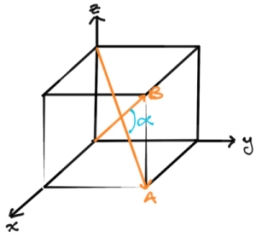
Úhel tělesových úhlopříček
Pomocí vektorového skalárního součinu (tečky) produktu vypočítejte úhel tělesových úhlopříček kostky.
Správná odpověď:
Tipy na související online kalkulačky
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Tělesových 7084
Vypočítej délky stěnových a tělesových úhlopříček kostky s délkou hrany 10cm. - Uhlopříčky
Vypočítejte délky stěnových a tělesových úhlopříček kvádru o rozměrech hran 0,5 m, 1 m a 2 m - Vypočítejte 2558
Vypočítejte velikost tělesových úhlopříček hranolu s podstavou kosočtverce, pokud velikosti úhlopříček podstavy jsou 16 cm a 20 cm a výška hranolu je 32 cm. Vypočítejte velikost hrany podstavy. - Uhlopríčky kostky Kostka má obsah stěny 81 cm čtverečních. Vypočítejte délku její hrany, stěnové a tělesových úhlopříčky.
- Krychle - stěna
Vypočtěte tělesových úhlopříčku kostky, pokud víte, že povrch jedné její stěny se rovná 36 centimetrů čtverečních. Prosím, vypočítejte její objem. - Kvádr
Vypočítejte úhel který svírá podstava kvádru 10 × 10 s tělesových úhlopříčkou dlouhou 19. - Kostka - úhly
Vypočítejte úhel alfa (α) mezi stěnovou úhlopříčkou a podstavou krychle. Vypočítejte úhel beta (β) mezi tělesových úhlopříčkou a podstavou krychle.
