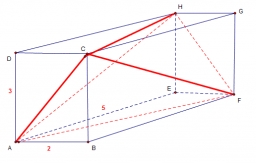
Wall and body diagonals
Calculate the lengths of the wall and body diagonals of the cuboid with edge dimensions of 0.5 m, 1 m, and 2 m
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
solid geometryplanimetricsGrade of the word problem
Related math problems and questions:
- Rotational motion of a cylinder
Calculate the kinetic energy of a cylindrical body of radius r= 0.08 meter and mass m= 1.5kg at time t= 5 s, if this body rotates around an axis passing through the center of the cylinder with a constant acceleration Ԑ= 5 rad/s², if at time t=. - Diagonals 7084
Calculate the lengths of the wall and body diagonals of the cube with an edge length of 10 cm. - Cuboid diagonals
The cuboid has dimensions of 15, 20, and 40 cm. Calculate its volume and surface, the length of the body diagonal, and the lengths of all three wall diagonals. - A bus 2
A bus traveled from Town A to Town B. The whole journey, 240 km, started at 1:00 p.m. and ended at 5:00 p.m. Find the average bus speed. - At noon 4
At noon, the temperature was 9ºC. Between noon and 11:00 p.m., it rose by 8ºC, fell by 4ºC, rose by 3ºC, and then fell by 8ºC. What was the temperature at 11:00 p.m.? - Calculate 80793
The liquid has a specific gravity of γ = 9050 N. m-3. Calculate its specific gravity, the mass of 2 m³ of this liquid, and also of 3 m³ of this liquid. - Wall and body diagonals
The block/cuboid has dimensions a = 4cm, b = 3cm, and c = 12cm. Calculate the length of the wall and body diagonals.
