Wall and body diagonals
The block/cuboid has dimensions a = 4cm, b = 3cm, and c = 12cm. Calculate the length of the wall and body diagonals.
Correct answer:
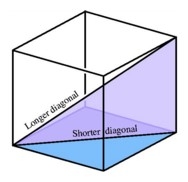
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Dimensions 4703
The block has dimensions l = 5 cm, w = 4 cm, and h = 3 cm. Calculate the length of its body diagonal. - Cuboid diagonals
The cuboid has dimensions of 15, 20, and 40 cm. Calculate its volume and surface, the length of the body diagonal, and the lengths of all three wall diagonals. - The block
The block has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this block. - Body diagonal
Calculate the length of the body diagonal of a block with dimensions: a = 20 cm, b = 30 cm, c = 15 cm.
- Wall and body diagonals
Calculate the lengths of the wall and body diagonals of the cuboid with edge dimensions of 0.5 m, 1 m, and 2 m - Dimensions 48161
A block with dimensions a = 15cm b = 5cm and a block height c = 8cm. Calculate the length of the wall diagonal in the base. - Dimensions 80753
We color a wooden block with dimensions a = 4 cm, b = 3 cm, c = 2 cm and then cut it into cubes of 1 cm³. How many cats will she have? a) just one wall painted b) just two walls stained c) just three walls painted d) no painted wall?
