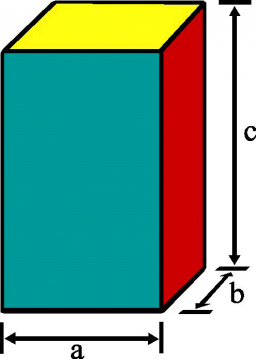
Quadrangular block
The surface of the quadrilateral block is 3.4 dm2. The edges of the block are 8 cm and 10 cm long. Calculate the volume of the block.
Final Answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
solid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Block surface ratio
The volume of the block is 7,500 dm³. The lengths of the edges are in the ratio 3: 4: 5. Calculate the surface area of the cuboid. - Prism height calculation
Calculate the height of a regular quadrilateral prism whose base is a rhombus. The edge in the base is 7 cm long, the opposite edges are 5 cm apart, and we also know that the entire body has a volume of 1dm³. - Cuboid and cube
A block with edges of lengths of 10 cm and 8 cm has the same volume as a cube with an edge of the length of 1 dm. Calculate the third dimension of the block. Compare the ratio of the surfaces of both bodies. - Block diagonal
Calculate the length of the body diagonal of a block whose two edges are 2 cm and 7 cm long and whose volume is equal to 49 cubic centimeters. - Cuboid Dimensions Ratio Surface
The base of a cuboid is a rectangle. The ratio of its length to width is 3:2. The length of the rectangle of the base is in the ratio of 4:5 to the height of the block. The sum of the lengths of all the edges of the block is 2.8m. Find: a) the surface of - Pyramid measurements
Calculate the surface area and volume of a regular quadrilateral truncated pyramid if the base edges are 87 cm and 64 cm and the wall height is 49 cm. - Pyramid Height Surface Area
The regular quadrilateral pyramid has a base diagonal of 5√2 cm, and the side edges are 12√2 cm long. Calculate the height of the pyramid and its surface.
