Smaller square
Let the points A, B, C and D are midpoints of the sides of the square PQRS. If the area of PQRS is 100 sq cm, what is the area of the smaller square ABCD?
Final Answer:

Tips for related online calculators
Do you want to convert length units?
The Pythagorean theorem is the base for the right triangle calculator.
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Parallelogram ABCD
 The area of parallelogram ABCD is 906 cm². Points M and N are the midpoints of the sides AB and BC. What is the area of a quadrilateral MBND?
The area of parallelogram ABCD is 906 cm². Points M and N are the midpoints of the sides AB and BC. What is the area of a quadrilateral MBND? - Connecting lines
 They are given a square ABCD. The points EFGH are the midpoints of its sides. What part of the area of the square ABCD is the area of the square created in its center by connecting the points AF, BG, CH, and DE?
They are given a square ABCD. The points EFGH are the midpoints of its sides. What part of the area of the square ABCD is the area of the square created in its center by connecting the points AF, BG, CH, and DE? - The square - midpoints
 The area of a square ABCD is 36 cm². Find the area of the square obtained by joining the midpoints of the sides of the square ABCD.
The area of a square ABCD is 36 cm². Find the area of the square obtained by joining the midpoints of the sides of the square ABCD. - Midpoint triangle
 Triangle ABC is equilateral with a side length of 8 cm. Points D, E, and F are the sides AB, BC, and AC midpoints. Calculate the area of triangle DEF. In what ratio is the area of triangle ABC to the area of triangle DEF?
Triangle ABC is equilateral with a side length of 8 cm. Points D, E, and F are the sides AB, BC, and AC midpoints. Calculate the area of triangle DEF. In what ratio is the area of triangle ABC to the area of triangle DEF? - Square triangle area
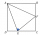 The area of the ABCD square in the picture is 36 cm². Points E and F are the centers of the square BC and CD sides. What is the area of the triangle AEF in cm²?
The area of the ABCD square in the picture is 36 cm². Points E and F are the centers of the square BC and CD sides. What is the area of the triangle AEF in cm²? - The areas
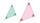 The areas of two similar triangles are 12 sq cm and 48 sq cm. If the height of the smaller one is 2.1 cm, then find the height of the bigger one.
The areas of two similar triangles are 12 sq cm and 48 sq cm. If the height of the smaller one is 2.1 cm, then find the height of the bigger one. - Rectangle - parallelogram
 A rectangle is circumscribed by a circle with a radius of 5 cm. The short side of the rectangle measures 6 cm. Calculate the perimeter of a parallelogram ABCD, whose vertices are the midpoints of the sides of the rectangle.
A rectangle is circumscribed by a circle with a radius of 5 cm. The short side of the rectangle measures 6 cm. Calculate the perimeter of a parallelogram ABCD, whose vertices are the midpoints of the sides of the rectangle.
