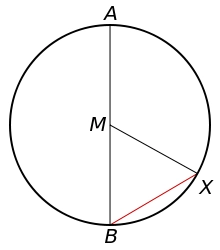
A chord 2
A chord of length 16 cm is drawn in a circle of radius 10 cm. Calculate the distance of the chord from the center of the circle.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Calculate 79144
The circle's radius is r=8.9 cm, and the chord AB of this circle has a length of 16 cm. Calculate the distance of chord AB from the center of the circle. - Two chords
Two parallel chords are drawn in a circle with a radius r = 26 cm. One chord has a length of t1 = 48 cm, and the second has a length of t2 = 20 cm, with the center lying between them. Calculate the distance between two chords. - Intersection 83575
Given a circle with a radius r = 4 cm and a point A for which |AS| applies = 10 cm. Calculate the distance of point A from the intersection of the points of contact of the tangents drawn from point A to the circle. - Touch circle
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l
- Calculate 3561
There is a 12 cm long chord in a circle with a radius of 10 cm. Calculate the distance of the chord from the center of the circle. - A chord In a circle radius of 6 cm, a chord is drawn 3 cm from the center. Calculate the angle subtended by the cord at the center of the circle Hence find the length of the minor arc cut off by the chord.
- Circle chord
Calculate the length of the chord of the circle with radius r = 10 cm, the length of which is equal to the distance from the circle's center.
