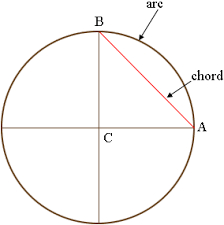
Calculate the chord
The circle's radius is r=8.9 cm, and the chord AB of this circle has a length of 16 cm. Calculate the distance of chord AB from the center of the circle.
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsGrade of the word problem
Related math problems and questions:
- Chord 2
Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle. - Circle chord
Calculate the length of the chord of the circle with radius r = 10 cm, the length of which is equal to the distance from the circle's center. - The chord
Calculate a chord length where the distance from the circle's center (S, 24 cm) equals 16 cm. - Chord length
Calculate the length of the circle chord, which is 2.5 cm from the circle's center. The radius is 6.5 cm. - A chord 2
A chord of length 16 cm is drawn in a circle of radius 10 cm. Calculate the distance of the chord from the center of the circle. - Circle radius calculation
Point B is the center of the circle. The line AC touches the circles at point C and applies AB = 20 cm and AC = 16 cm. What is the radius of the circle BC? - Circle length
The 16 cm long string is 6 cm from the circle's center. Calculate the length of the circle.
