Calculate 3561
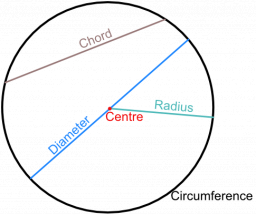
There is a 12 cm long chord in a circle with a radius of 10 cm. Calculate the distance of the chord from the center of the circle.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Circle chord
Calculate the length of the chord of the circle with radius r = 10 cm, the length of which is equal to the distance from the circle's center. - Calculate 80636
Calculate the distance of a chord 19 cm long from the center of a circle with a diameter of 28 cm. - Chord 2
Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle. - Calculate 79144
The circle's radius is r=8.9 cm, and the chord AB of this circle has a length of 16 cm. Calculate the distance of chord AB from the center of the circle. - Chord 3
The chord is 2/3 of the circle's radius from the center and has a length of 10 cm. How long is the circle radius? - String 63794
The chord AB is in the circle k with a radius of 13 cm. The center C of the string AB is 5 cm from the center S of the circle. How long is the AB string? - Chord
In a circle with a radius r=60 cm is the chord, 4× longer than its distance from the center. What is the length of the chord? - Magnitude 25411
There is a circle with a radius of 10 cm and its chord, which is 12 cm long. Calculate the magnitude of the central angle that belongs to this chord. - Chord MN
Chord MN of the circle has distance from the center circle S 120 cm. Angle MSN is 64°. Determine the radius of the circle. - Calculate 2577
Calculate the length of the circle chord, which is 2.5 cm from the circle's center. The radius is 6.5 cm. - Two chords
Two parallel chords are drawn in a circle with a radius r = 26 cm. One chord has a length of t1 = 48 cm, and the second has a length of t2 = 20 cm, with the center lying between them. Calculate the distance between two chords. - Circle chord
Determine the circle's radius in which the chord 6 cm away from the center is 12 cm longer than the circle's radius. - The chord
Calculate a chord length where the distance from the circle's center (S, 6 cm) equals 3 cm. - Circles
In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both). - Chord distance The circle k (S, 6 cm) calculates the chord distance from the center circle S when the chord length is t = 10 cm.
- Touch circle
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - Common chord
The common chord of the two circles, c1 and c2, is 3.8 cm long. This chord forms an angle of 47° with the radius r1 in the circle c1. An angle of 24° 30' with the radius r2 is formed in the circle c2. Calculate both radii and the distance between the two
