Chord practice problems
A chord of a circle is a straight line segment whose endpoints both lie on the circle. A chord that passes through a circle's center point is the circle's diameter. The word chord is from the Latin chorda meaning bowstring.Direction: Solve each problem carefully and show your solution in each item.
Number of problems found: 79
- Three inscribed objects
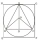 A circle is inscribed in a square. An equilateral triangle of side 4√3 is inscribed in that circle. Find the length of the diagonal of the square.
A circle is inscribed in a square. An equilateral triangle of side 4√3 is inscribed in that circle. Find the length of the diagonal of the square. - Two chords 2
 The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm away from the center of the circle, calculate the length of the second chord.
The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm away from the center of the circle, calculate the length of the second chord. - Two chords 6
 A chord PQ is 10.4cm long, and its distance from the center of a circle is 3.7cm. Calculate the length of a second chord RS, which is 4.1cm from the center of this circle.
A chord PQ is 10.4cm long, and its distance from the center of a circle is 3.7cm. Calculate the length of a second chord RS, which is 4.1cm from the center of this circle. - A chord 2
 A chord of length 16 cm is drawn in a circle of radius 10 cm. Calculate the distance of the chord from the center of the circle.
A chord of length 16 cm is drawn in a circle of radius 10 cm. Calculate the distance of the chord from the center of the circle. - Chords
 How many 5-tónových chords (chord = at the same time sounding different tones) is possible to play within 10 tones?
How many 5-tónových chords (chord = at the same time sounding different tones) is possible to play within 10 tones? - Endless lego set
 The endless Lego set contains only 6, 9, and 20-kilogram blocks that can no longer be polished or broken. The workers took them to the gym and immediately started building different buildings. And, of course, they wrote down how much the building weighed.
The endless Lego set contains only 6, 9, and 20-kilogram blocks that can no longer be polished or broken. The workers took them to the gym and immediately started building different buildings. And, of course, they wrote down how much the building weighed. - Chord of triangle
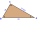 If the whole chord of the triangle is 14.4 cm long, how do you calculate the shorter and longer parts?
If the whole chord of the triangle is 14.4 cm long, how do you calculate the shorter and longer parts? - Circle's chords
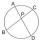 The circle has two chord lengths, 30 and 34 cm. The shorter one is from the center twice as a longer chord. Determine the radius of the circle.
The circle has two chord lengths, 30 and 34 cm. The shorter one is from the center twice as a longer chord. Determine the radius of the circle. - Circle chord
 Determine the circle's radius in which the chord 15 cm away from the center is 21 cm longer than the circle's radius.
Determine the circle's radius in which the chord 15 cm away from the center is 21 cm longer than the circle's radius. - Height of the arc - formula
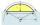 Calculate the arc's height if the arc's length is 65 and the chord length is 33. Does there exist a formula to solve this?
Calculate the arc's height if the arc's length is 65 and the chord length is 33. Does there exist a formula to solve this? - Chord 5
 It is given a circle k/S; 5 cm /. Its chord MN is 3 cm away from the center of the circle. Calculate its length.
It is given a circle k/S; 5 cm /. Its chord MN is 3 cm away from the center of the circle. Calculate its length. - Construct 83195
 Two line segments of different lengths are given. Construct a circle k so that both line segments are its chords.
Two line segments of different lengths are given. Construct a circle k so that both line segments are its chords. - Chord 3
 The chord is 2/3 of the circle's radius from the center and has a length of 10 cm. How long is the circle radius?
The chord is 2/3 of the circle's radius from the center and has a length of 10 cm. How long is the circle radius? - Chord distance
 The circle k (S, 6 cm) calculates the chord distance from the center circle S when the chord length is t = 10 cm.
The circle k (S, 6 cm) calculates the chord distance from the center circle S when the chord length is t = 10 cm. - Intersections 68784
 The figure shows the circles k₁(S₁; r1=9 cm) and k₂(S2; r2 = 5 cm). Their intersections determine a common chord t 8 cm long. Calculate the center distance |S₁ S₂| in cm to two decimal places.
The figure shows the circles k₁(S₁; r1=9 cm) and k₂(S2; r2 = 5 cm). Their intersections determine a common chord t 8 cm long. Calculate the center distance |S₁ S₂| in cm to two decimal places. - Intersect 6042
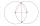 Two circles with straight radii of 58 mm intersect at two points. Their common string is 80 mm long. What is the distance of the centers of these circles?
Two circles with straight radii of 58 mm intersect at two points. Their common string is 80 mm long. What is the distance of the centers of these circles? - Circle
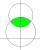 The circle is given by the center on S[-7; 10], and the maximum chord is 13 long. How many intersections have a circle with the coordinate axes?
The circle is given by the center on S[-7; 10], and the maximum chord is 13 long. How many intersections have a circle with the coordinate axes? - Two chords
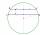 In a circle with a radius of 8.5 cm, two parallel chords are constructed, the lengths of which are 9 cm and 12 cm. Find the distance of the chords in a circle.
In a circle with a radius of 8.5 cm, two parallel chords are constructed, the lengths of which are 9 cm and 12 cm. Find the distance of the chords in a circle. - Perpendicular diameters
 Draw a circle k/S; 4.5 cm/. Next, draw: a/two mutually perpendicular diameters AB and CD b/two radii SA and SE which form an angle of 75 degrees c/chord/KL/= 4 cm d/chord/MN/, which is perpendicular to KL
Draw a circle k/S; 4.5 cm/. Next, draw: a/two mutually perpendicular diameters AB and CD b/two radii SA and SE which form an angle of 75 degrees c/chord/KL/= 4 cm d/chord/MN/, which is perpendicular to KL - Chord 2
 Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle.
Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
