Intersect 6042
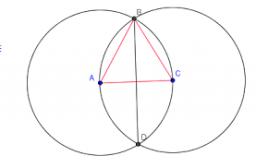
Two circles with straight radii of 58 mm intersect at two points. Their common string is 80 mm long. What is the distance of the centers of these circles?
Correct answer:
Showing 1 comment:
Cjinct
Unless I am missing something, triangle ABC is an equilateral triangle since all three sides are radii and therefore are congruent. If I am correct, you only need to know the length of the radii to answer the question ... AC = 58 cm and BD = 58(root 3) cm.
Please advise.
Please advise.
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Common chord
Two circles with radii 18 cm and 20 cm intersect at two points. Its common chord is long 11 cm. What is the distance of the centers of these circles? - Centimeters 7406
Circles with radii r1 = 10 centimeters and r2 = 4 cm touch from the outside. What is the distance between their centers? - Intersections 2557
How many intersections do circles with radii of 10 cm and 6 cm have if the distance between their centers is 3 cm? - Common chord
The common chord of the two circles, c1 and c2, is 3.8 cm long. This chord forms an angle of 47° with the radius r1 in the circle c1. An angle of 24° 30' with the radius r2 is formed in the circle c2. Calculate both radii and the distance between the two
- Intersections
How many intersections have circles with radius 16 mm and 15 mm if the distance of their centers is 16 mm? - Two circles
Two circles with a radius of 4 cm and 3 cm have a center distance of 0.5cm. How many common points have these circles? - Construct 83156
Construct 2 circles so that their centers are 5 cm apart and: and they had no common touch b- they had a common point They had 2 points in common.
