Circle
The circle is given by the center on S[-7; 10], and the maximum chord is 13 long.
How many intersections have a circle with the coordinate axes?
How many intersections have a circle with the coordinate axes?
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Intersections 49433
Draw a graph of the function given by the equation y = -2x +3, determine its intersections with the coordinate axes, and complete the missing coordinates A [3;? ], B [?; 8]. - Chord BC
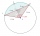A circle k has the center at the point S = [0; 0]. Point A = [40; 30] lies on the circle k. How long is the chord BC if the center P of this chord has the coordinates [- 14; 0]? - Intersections
Find the intersections of the function plot with coordinate axes: f (x): y = x + 3/5 - Subtended 83194
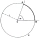A circle k with a center at point S and a radius of 6 cm is given. Calculate the size of the central angle subtended by a chord 10 cm long.
- Coordinate axes
Find the triangle area given by line -7x+7y+63=0 and coordinate axes x and y. - Calculate 3561
There is a 12 cm long chord in a circle with a radius of 10 cm. Calculate the distance of the chord from the center of the circle. - Perpendicular 82994
The straight line p is given by the formula y = 1/2 x - 1 . The line q is perpendicular to the line p and passes through the point A [1; 5]. Determine the y-coordinate of the point that intersects the line q with the y-axis.
