Chord practice problems - page 2 of 4
Direction: Solve each problem carefully and show your solution in each item.Number of problems found: 79
- Two parallel chords
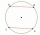The two parallel chords of the circle have the same length of 6 cm and are 8 cm apart. Calculate the radius of the circle. - String 63794
The chord AB is in the circle k with a radius of 13 cm. The center C of the string AB is 5 cm from the center S of the circle. How long is the AB string? - Calculate 3562
The 16 cm long string is 6 cm from the circle's center. Calculate the length of the circle. - Chord 4
I need to calculate the circumference of a circle, and I know the chord length c=22 cm and the distance from the center d=29 cm chord to the circle. - Two chords
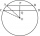Two parallel chords are drawn in a circle with a radius r = 26 cm. One chord has a length of t1 = 48 cm, and the second has a length of t2 = 20 cm, with the center lying between them. Calculate the distance between two chords. - Calculate chord A circle k (S, 5cm) is given. Calculate the length of the chord of the circle k if it is 3 cm from the center S.
- Concentric circles and chord
In a circle with a diameter d = 10 cm, a chord with a length of 6 cm is constructed. What radius has the concentric circle while touching this chord? - The fence
I'm building a cloth (board) fence. The boards are rounded in a semicircle at the top. The tops of the boards between the columns should copy an imaginary circle. The tip of the first and last board forms the chord of a circle whose radius is unknown. The - Two chords
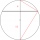Calculate the length of chord AB and perpendicular chord BC to the circle if AB is 4 cm from the circle's center and BC 8 cm from the center. - Meneal's 26771
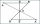Show (using Meneal's theorem) that the center of gravity divides the line in a 1:2 ratio. - Two parallel chords
In a circle 70 cm in diameter, two parallel chords are drawn so that the circle's center lies between the chords. Calculate the distance of these chords if one is 42 cm long and the second is 56 cm long. - Calculate 3561
There is a 12 cm long chord in a circle with a radius of 10 cm. Calculate the distance of the chord from the center of the circle. - Chord AB
What is the chord AB's length if its distance from the center S of the circle k(S, 50 cm) is 43 cm? - Chord
In a circle with a radius r=60 cm is the chord, 4× longer than its distance from the center. What is the length of the chord? - Common chord
The common chord of the two circles, c1 and c2, is 3.8 cm long. This chord forms an angle of 47° with the radius r1 in the circle c1. An angle of 24° 30' with the radius r2 is formed in the circle c2. Calculate both radii and the distance between the two - Determine 6415
Determine the distance of two parallel chords of lengths of 7 cm and 11 cm in a circle with a radius of 7 cm. - Tangent
What distance are the tangent t of the circle (S, 4 cm) and the chord of this circle, which is 6 cm long and parallel to the tangent t? - Construction 32971
There is any circle k that does not have a marked center. Use a suitable construction to find the center of the circle k. Try on two different circles. - Intersection + tangents
Given a circle with a radius r = 4 cm and a point A for which |AS| applies = 10 cm. Calculate the distance of point A from the intersection of the points of contact of the tangents drawn from point A to the circle. - Chord
The point on the circle is the endpoint of diameter and endpoint of the chord length of the radius. What angle between chord and diameter?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
