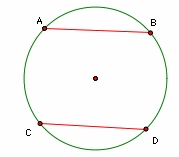
Two parallel chords
The two parallel chords of the circle have the same length of 6 cm and are 8 cm apart. Calculate the radius of the circle.
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
planimetricsGrade of the word problem
Related math problems and questions:
- Chord distance
Two parallel chords in a circle with a radius of 6 cm have lengths of 6 cm and 10 cm. Calculate their distance from each other. Find both solutions. - Two chords
Two parallel chords are drawn in a circle with a radius r = 26 cm. One chord has a length of t1 = 48 cm, and the second has a length of t2 = 20 cm, with the center lying between them. Calculate the distance between two chords. - Circles
In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both). - Two chords
In a circle with a radius of 8.5 cm, two parallel chords are constructed, the lengths of which are 9 cm and 12 cm. Find the distance of the chords in a circle. - Chord distance
Determine the distance of two parallel chords of lengths of 7 cm and 11 cm in a circle with a radius of 7 cm. - Two parallel chords
In a circle 70 cm in diameter, two parallel chords are drawn so that the circle's center lies between the chords. Calculate the distance of these chords if one is 42 cm long and the second is 56 cm long. - Chord distance length
The radius of the circle is 5.5 cm. The height is 2.3 cm, which is the chord's distance. How can we calculate the length of the string?
