Chord practice problems - page 3 of 4
Direction: Solve each problem carefully and show your solution in each item.Number of problems found: 79
- Chord 4
 I need to calculate the circumference of a circle, and I know the chord length c=16 cm and the distance from the center d=15 cm chord to the circle.
I need to calculate the circumference of a circle, and I know the chord length c=16 cm and the distance from the center d=15 cm chord to the circle. - Common chord
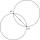 Two circles with radii 18 cm and 20 cm intersect at two points. Its common chord is long 11 cm. What is the distance of the centers of these circles?
Two circles with radii 18 cm and 20 cm intersect at two points. Its common chord is long 11 cm. What is the distance of the centers of these circles? - Calculate the chord
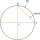 The circle's radius is r=8.9 cm, and the chord AB of this circle has a length of 16 cm. Calculate the distance of chord AB from the center of the circle.
The circle's radius is r=8.9 cm, and the chord AB of this circle has a length of 16 cm. Calculate the distance of chord AB from the center of the circle. - Magnitude 25411
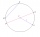 There is a circle with a radius of 10 cm and its chord, which is 12 cm long. Calculate the magnitude of the central angle that belongs to this chord.
There is a circle with a radius of 10 cm and its chord, which is 12 cm long. Calculate the magnitude of the central angle that belongs to this chord. - Circle chord
 What is the length x of the chord circle of diameter 115 m if the distance from the center circle is 11 m?
What is the length x of the chord circle of diameter 115 m if the distance from the center circle is 11 m? - Length of the chord
 Calculate the length of the chord in a circle with a radius of 25 cm and a central angle of 26°.
Calculate the length of the chord in a circle with a radius of 25 cm and a central angle of 26°. - Two chords
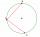 There is a given circle k (center S, radius r). From point A, which lies on circle k, are starting two chords of length r. What angle do chords make? Draw and measure.
There is a given circle k (center S, radius r). From point A, which lies on circle k, are starting two chords of length r. What angle do chords make? Draw and measure. - Calculate 3561
 There is a 12 cm long chord in a circle with a radius of 10 cm. Calculate the distance of the chord from the center of the circle.
There is a 12 cm long chord in a circle with a radius of 10 cm. Calculate the distance of the chord from the center of the circle. - Chord and radius
 Calculate the radius of a circle whose chord XY is 8 cm long and whose center is 3 cm from the chord.
Calculate the radius of a circle whose chord XY is 8 cm long and whose center is 3 cm from the chord. - The chord
 Calculate a chord length where the distance from the circle's center (S, 24 cm) equals 16 cm.
Calculate a chord length where the distance from the circle's center (S, 24 cm) equals 16 cm. - Circles
 In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both).
In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both). - Two chords
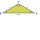 From the point on the circle with a diameter of 8 cm, two identical chords are led, which form an angle of 60°. Calculate the length of these chords.
From the point on the circle with a diameter of 8 cm, two identical chords are led, which form an angle of 60°. Calculate the length of these chords. - Calculate 80636
 Calculate the distance of a chord 19 cm long from the center of a circle with a diameter of 28 cm.
Calculate the distance of a chord 19 cm long from the center of a circle with a diameter of 28 cm. - Calculate 2577
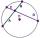 Calculate the length of the circle chord, which is 2.5 cm from the circle's center. The radius is 6.5 cm.
Calculate the length of the circle chord, which is 2.5 cm from the circle's center. The radius is 6.5 cm. - Chord MN
 Chord MN of the circle has distance from the center circle S 28 cm. Angle MSN is 54°. Determine the radius of the circle.
Chord MN of the circle has distance from the center circle S 28 cm. Angle MSN is 54°. Determine the radius of the circle. - Central angle
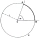 A circle k with a center at point S and a radius of 6 cm is given. Calculate the size of the central angle subtended by a chord 10 cm long.
A circle k with a center at point S and a radius of 6 cm is given. Calculate the size of the central angle subtended by a chord 10 cm long. - Chords centers
 The circle has a diameter of 17 cm, upper chord |CD| = 10.2 cm, and bottom chord |EF| = 7.5 cm. The chords H and G midpoints are |EH| = 1/2 |EF| and |CG| = 1/2 |CD|. Find the distance between the G and H if CD II EF (parallel).
The circle has a diameter of 17 cm, upper chord |CD| = 10.2 cm, and bottom chord |EF| = 7.5 cm. The chords H and G midpoints are |EH| = 1/2 |EF| and |CG| = 1/2 |CD|. Find the distance between the G and H if CD II EF (parallel). - Sprinkler - irrigated area
 A sprinkler is located in the park at a distance of 3m from the sidewalk. Water blasted up to a distance of max. 5m. What is the maximum length of the sidewalk it will cover?
A sprinkler is located in the park at a distance of 3m from the sidewalk. Water blasted up to a distance of max. 5m. What is the maximum length of the sidewalk it will cover? - Chord
 It is given to a circle k(r=6 cm), and the points A and B such that |AB| = 8 cm lie on k. Calculate the distance of the center of circle S to the midpoint C of segment AB.
It is given to a circle k(r=6 cm), and the points A and B such that |AB| = 8 cm lie on k. Calculate the distance of the center of circle S to the midpoint C of segment AB. - The chord
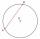 A chord passing through its center is the side of the triangle inscribed in a circle. What size are a triangle's internal angles if one is 40°?
A chord passing through its center is the side of the triangle inscribed in a circle. What size are a triangle's internal angles if one is 40°?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
