Two chords
From the point on the circle with a diameter of 8 cm, two identical chords are led, which form an angle of 60°. Calculate the length of these chords.
Final Answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
See also our right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Two chords
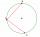 There is a given circle k (center S, radius r). From point A, which lies on circle k, are starting two chords of length r. What angle do chords make? Draw and measure.
There is a given circle k (center S, radius r). From point A, which lies on circle k, are starting two chords of length r. What angle do chords make? Draw and measure. - Chord 2
 Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle.
Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle. - Track arc
 Two straight tracks are at an angle 126°. They will join with a circular arc with a radius r=1110 m. How long will the arc be connecting these lines (L)? How far is the arc's center point from track crossings (x)?
Two straight tracks are at an angle 126°. They will join with a circular arc with a radius r=1110 m. How long will the arc be connecting these lines (L)? How far is the arc's center point from track crossings (x)? - Two parallel chords
 In a circle 70 cm in diameter, two parallel chords are drawn so that the circle's center lies between the chords. Calculate the distance of these chords if one is 42 cm long and the second is 56 cm long.
In a circle 70 cm in diameter, two parallel chords are drawn so that the circle's center lies between the chords. Calculate the distance of these chords if one is 42 cm long and the second is 56 cm long. - Mass point
 Two equal forces of 30 Newtons act on a mass point. Find the magnitude of the resultant force if these forces form an angle of 42°.
Two equal forces of 30 Newtons act on a mass point. Find the magnitude of the resultant force if these forces form an angle of 42°. - Circles
 In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both).
In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both). - Two parallel chords
 The two parallel chords of the circle have the same length of 6 cm and are 8 cm apart. Calculate the radius of the circle.
The two parallel chords of the circle have the same length of 6 cm and are 8 cm apart. Calculate the radius of the circle.
