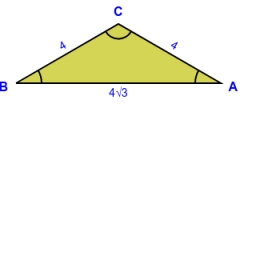
Tetivy pod uhlom
Z bodu na kružnici s priemerom 8 cm sú vedené dve zhodné tetivy, ktoré zvierajú uhol 60°. Vypočítaj dĺžku týchto tetív.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Hľadáte pomoc s výpočtom koreňov kvadratickej rovnice?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraplanimetriagoniometria a trigonometriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- V kružnici 2
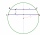 V kružnici s priemerom 70 cm sú narysované dve rovnobežné tetivy tak, že stred kružnice leží medzi tetivami. Vypočítaj vzdialenosť týchto tetív, ak jedna z nich má dĺžku 42 cm a druhá 56 cm.
V kružnici s priemerom 70 cm sú narysované dve rovnobežné tetivy tak, že stred kružnice leží medzi tetivami. Vypočítaj vzdialenosť týchto tetív, ak jedna z nich má dĺžku 42 cm a druhá 56 cm. - Dve tetivy 2
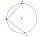 Je daná kružnica k (S, r). Z bodu A ktorý patrí k idú dve tetivy s dľžkou r. Aký uhol zvierajú? Narysuj a odmeraj.
Je daná kružnica k (S, r). Z bodu A ktorý patrí k idú dve tetivy s dľžkou r. Aký uhol zvierajú? Narysuj a odmeraj. - Dve tetivy
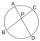 V kružnici sú vedené dve tetivy dlhé 30 a 34 cm. Kratšia z nich je od stredu dvakrát ďalej než dlhšia. Urči polomer kružnice.
V kružnici sú vedené dve tetivy dlhé 30 a 34 cm. Kratšia z nich je od stredu dvakrát ďalej než dlhšia. Urči polomer kružnice. - Vypočítajte 64
 Vypočítajte dĺžku tetivy v kružnici s polomerom 25 cm, ktorej prislúcha obvodový uhol 26°.
Vypočítajte dĺžku tetivy v kružnici s polomerom 25 cm, ktorej prislúcha obvodový uhol 26°. - Dve rovnobežné
 Dve rovnobežné tetivy kružnice majú rovnakú dĺžku 6 cm a sú od seba vzdialené 8 cm. Vypočítaj polomer kružnice.
Dve rovnobežné tetivy kružnice majú rovnakú dĺžku 6 cm a sú od seba vzdialené 8 cm. Vypočítaj polomer kružnice. - Tetiva
 V kružnici s polomerom 10 cm je 12 cm dlhá tetiva. Vypočítaj vzdialenosť tetivy od stredu kružnice.
V kružnici s polomerom 10 cm je 12 cm dlhá tetiva. Vypočítaj vzdialenosť tetivy od stredu kružnice. - Tetiva 2
 Bod A má od stredu kružnice s polomerom r = 5 cm vzdialenosť 13 cm. Vypočítajte dĺžku tetivy spájajúca body dotyku T1 a T2 dotyčníc vedených z bodu A ku kružnici k.
Bod A má od stredu kružnice s polomerom r = 5 cm vzdialenosť 13 cm. Vypočítajte dĺžku tetivy spájajúca body dotyku T1 a T2 dotyčníc vedených z bodu A ku kružnici k.
