V kružnici 2

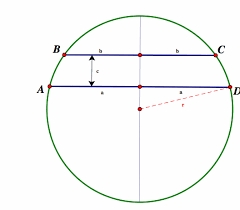
V kružnici s priemerom 70 cm sú narysované dve rovnobežné tetivy tak, že stred kružnice leží medzi tetivami. Vypočítaj vzdialenosť týchto tetív, ak jedna z nich má dĺžku 42 cm a druhá 56 cm.

Správny výsledok:

v₁ =  49 cm
v₂ =  7 cm

Riešenie:

$$\begin{gathered} d=70\text{ cm } \\ r=d\mathrm{/}2=70\mathrm{/}2=35\text{ cm } \\ {t}_1=42\text{ cm } \\ {t}_2=56\text{ cm } \\ {x}_1=\sqrt{r^2-(t_1\mathrm{/}2{)}^2}=\sqrt{35^2-(42\mathrm{/}2{)}^2}=28\text{ cm } \\ {x}_2=\sqrt{r^2-(t_2\mathrm{/}2{)}^2}=\sqrt{35^2-(56\mathrm{/}2{)}^2}=21\text{ cm } \\ {v}_1=x_2+x_1=21+28=49\text{ cm} \end{gathered}$$

$v_2=\mathrm{\mid }{x}_2-x_1\mathrm{\mid }=\mathrm{\mid }21-28\mathrm{\mid }=7\text{ cm}$

Skúsiť iný príklad

Zobrazujem 0 komentárov:

Ďaľšie podobné príklady a úlohy:

• Dve tetivy 4
  V kružnici s r=26 cm sú narysované 2 rovnobežné tetivy . Jedna tetiva má dĺžku t₁=48 cm a druhá má dĺžku t₂=20cm, pričom stred leží medzi nimi. Vypočítaj vzdialenosť dvoch tetív.
• Tetiva 17
  Akú vzdialenosť majú dotyčnica t kružnice (S, 4 cm) a tetiva tejto kružnice, ktorá má dlžku 6 cm a je rovnobežná s dotyčnicou?
• Tetivy
  V kružnici s polomerom 8,5 cm sú zostrojené dve rovnobežné tetivy, ktorých dĺžky sú 9 cm a 12 cm. Vypočítajte vzdialenosť tetív v kružnici.
• Kružnice
  V kružnici s polomerom 7,5 cm sú zostrojené 2 rovnobežné tetivy, ktorých dĺžky sú 9 cm a 12 cm. Vypočítajte vzdialenosť týchto tetív (ak sú možné dve riešenia napíšte obe).
• Dve rovnobežné
  Dve rovnobežné tetivy kružnice majú rovnakú dĺžku 6 cm a sú od seba vzdialené 8 cm. Vypočítaj polomer kružnice.
• Tetiva
  Akú dĺžku x má tetiva kružnice s priemerom 60 m, ak je vzdialená od stredu kružnice 10 m?
• Tetivy pod uhlom
  Z bodu na kružnici s priemerom 8 cm sú vedené dve zhodné tetivy, ktoré zvierajú uhol 60°. Vypočítaj dĺžku týchto tetív.
• Tetiva
  Akú dĺžku má tetiva AB, ktorej vzdialenosť od stredu S kružnice k(S, 92 cm) sa rovná 10 cm?
• Sústredna kružnica
  V kružnici s priemerom 15 cm je zostrojená tetiva dĺžky 5 cm. Vypočítajte polomer sústrednej kružnice, ktorá sa dotýka tetivy.
• Tetiva
  V kružnici s polomerom 10 cm je 12 cm dlhá tetiva. Vypočítaj vzdialenosť tetivy od stredu kružnice.
• V kružnici
  V kružnici s priemerom d = 10 cm, je zostrojená tetiva o dĺžke 6 cm. Aký polomer by mala sústredná kružnica, ktorá by sa tejto tetivy dotýkala?
• Tetiva
  V kružnici k (S; 6cm) vypočítajte vzdialenosť tetivy t od stredu kružnice S, ak dĺžka tetivy je t= 10cm.
• Tetiva
  Vypočítaj dĺžku tetivy, ktorej vzdialenosť od stredu S kružnice k (S, 6 cm) sa rovná 3 cm.
• Tetiva 2
  Bod A má od stredu kružnice s polomerom r = 5 cm vzdialenosť 13 cm. Vypočítajte dĺžku tetivy spájajúca body dotyku T1 a T2 dotyčníc vedených z bodu A ku kružnici k.
• Tetiva 4
  Potrebujem vypočítať obvod kruhu, keď poznám dĺžku tetivy t=22 cm a vzdialenosť od stredu d=29 cm tetivy ku kružnici.
• Dve tetivy
  V kružnici sú vedené dve tetivy dlhé 30 a 34 cm. Kratšia z nich je od stredu dvakrát ďalej než dlhšia. Urči polomer kružnice.
• Tetiva 5
  Vypočítaj dĺžku tetivy kružnice, ktorá je vzdialená od stredu kružnice 2,5 cm. Polomer je 6,5 cm.