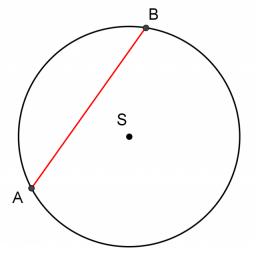
The chord
A chord passing through its center is the side of the triangle inscribed in a circle. What size are a triangle's internal angles if one is 40°?
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Internal and external angles
Calculate a triangle's remaining internal and external angles if you know the internal angle γ (gamma) = 34 degrees and one exterior angle is 78 degrees and 40 '. Determine what kind of triangle it is from the size of its angles. - Angles
The outer angle of the triangle ABC at vertex A is 147°12'. The outer angle at vertex B is 113°42'. What size is the internal angle at vertex C? - Calculate 83431
In triangle ABC, the size of the exterior angle at vertex C is equal to 126°. The size of the internal angles at vertices A and B are in the ratio 5: 9. Calculate the size of the internal angles α, β, γ of triangle ABC. - Area and two angles
Calculate the size of all sides and internal angles of a triangle ABC if it is given by area S = 501.9; and two interior angles α = 15°28' and β = 45°.
- Diamond and angles
The internal angles in the diamond are 60° and 120°. Its side is 5 cm long. Find the area of a diamond. - Triangle SAA
The triangle has one side long 23 m, and its two internal angles are 60°. Calculate the perimeter and area of the triangle. - Diagonals
Calculate the length of the rhombus's diagonals if its side is long 21 and one of its internal angles is 10°.
