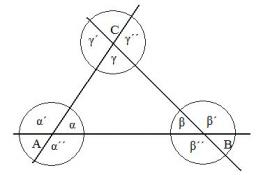
Internal and external angles
Calculate a triangle's remaining internal and external angles if you know the internal angle γ (gamma) = 34 degrees and one exterior angle is 78 degrees and 40 '. Determine what kind of triangle it is from the size of its angles.
Correct answer:
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Calculate 83431
In triangle ABC, the size of the exterior angle at vertex C is equal to 126°. The size of the internal angles at vertices A and B are in the ratio 5: 9. Calculate the size of the internal angles α, β, γ of triangle ABC. - Three angles
In a triangle ABC, the magnitude of the internal angle gamma is equal to one-third of the angle alpha. The size of the angle beta is 80 degrees larger than the size of the gamma angle. Calculate the magnitudes of the interior angles of the triangle ABC. - Determine 83240
In triangle ABC, the internal angle beta is twice the size of the angle alpha, and the angle gamma is 20 degrees less than the size of the angle beta. Determine the size of all interior angles of this triangle. - Triangle - angles
ABC triangle, alpha = 54 degrees 32 minutes, beta = 79 degrees. What are the sizes of the exterior angles?
- Alfa beta gama
The triangle's interior angle beta is 10 degrees greater than the angle alpha, and the gamma angle is three times larger than the beta. Determine the size of the interior angles. - The chord
A chord passing through its center is the side of the triangle inscribed in a circle. What size are a triangle's internal angles if one is 40°? - Area and two angles
Calculate the size of all sides and internal angles of a triangle ABC if it is given by area S = 501.9; and two interior angles α = 15°28' and β = 45°.
