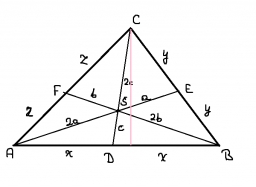
Meneal's 26771
Show (using Meneal's theorem) that the center of gravity divides the line in a 1:2 ratio.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
geometryalgebraplanimetricsbasic operations and conceptsthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Ratio of triangles areas
In an equilateral triangle ABC, the point T is its center of gravity, the point R is the image of the point T in axial symmetry along the line AB, and the point N is the image of the point T in axial symmetry along the line BC. Find the ratio of the areas - Isosceles 5575
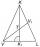The picture shows an isosceles triangle VLK with a center of gravity of T. The base VL measures 16 cm, and the line KK1 measures 18 cm. How long is the VV1 line? - Center
In the ABC triangle is point D[1,-2,6], which is the center of the |BC|, and point G[8,1,-3], which is the center of gravity of the triangle. Find the coordinates of the vertex A[x,y,z]. - Triangle 69144
The line p passes through the center of gravity T of the triangle and is parallel to the line BC. What is the ratio of the area of the divided smaller part of the triangle by the line p? What is the area of the triangle?
- The triangle
Three vertices give the triangle: A [0.0] B [-4.2] C [-6.0] Calculate V (intersection of heights), T (center of gravity), O - the center of a circle circumscribed - Centre of mass
The vertices of triangle ABC are from the line p distances 3 cm, 4 cm, and 8 cm. Calculate the distance from the center of gravity of the triangle to line p. - Calculate 4425
In the triangle ABC with the center of gravity T, b = 7cm, median to c: tc = 9cm, the ATC angle is 112 degrees. Calculate the length of the line ta.
