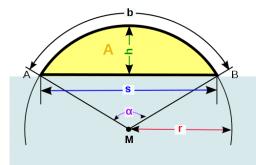
Height of the arc - formula
Calculate the arc's height if the arc's length is 65 and the chord length is 33.
Does there exist a formula to solve this?
Does there exist a formula to solve this?
Correct answer:
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to round the number?
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you want to convert length units?
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to round the number?
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Square and circles
The square in the picture has a side length of a = 20 cm. Circular arcs have centers at the vertices of the square. Calculate the areas of the colored unit. Express area using side a. - Convex angle
There is a circle k (S; r), and a point A, which lies on this circle. There is also a point B on the circumference, for which it is true that in one direction, it is five times further from point A than in the opposite direction (around the circumference - Circle's 81078
The chord of a circle is 233 long, and the length of the circular arc above the chord is 235. What is the circle's radius, and what is the central angle of the circular arc? - Aquarium height
How high does the water in the aquarium reach if there are 36 liters of water in it? The length of the aquarium is 60 cm, and the width is 4 dm.
- Circular segment
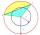Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ) - Derivation
Does there exist a function whose derivation is the same function? - Inscribed triangle
A circle is an inscribed triangle, and its vertices divide the circle into three arcs. The length of the arcs is in the ratio 2:3:7. Find the interior angles of a triangle.
