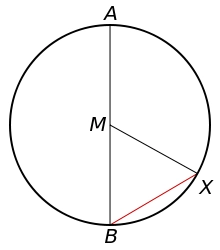
Circle and chord
The chord of a circle is 233 long, and the length of the circular arc above the chord is 235. What is the circle's radius, and what is the central angle of the circular arc?
Your answer:
Your answer:
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
Do you want to convert length units?
See also our right triangle calculator.
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you want to convert length units?
See also our right triangle calculator.
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
algebraplanimetrygoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Circle arc + section
Calculate the length of the arc of a circle and the volume of a circular section if the circle's radius is 8.3 centimeters and the central angle alpha=104 degrees. - Circle and angle
What is the arc length of a circle with radius r = 432 dm corresponding to a central angle of 0.53 rad? - Perimeter 59
The circumference of a circular bed is 36 m. Find the length of the arc corresponding to the following central angles: 90°, 45°30′, 120°, 15°. - Central angle 2 What is the arc length of a circle with a radius of 12 cm and a central angle of 255 degrees? A. 8.5 cm B. 12π cm C. 24π cm D. 17π cm
- Circle arc
A circular sector has an arc length of 7.16 m and an area of 146.69 m². Calculate the radius of the circle and the size of the central angle. - Arc
The arc of a circle corresponding to a central angle of 357° is 18 dm long. What is the circumference of the entire circle? - Circular segment
Calculate the area of a circular segment if the radius r = 80 cm and the central angle is α = 110°.
