Circular arc practice problems
A circular arc is a part of a circle defined by two end points lying on the circle. It is the intersection of a circle and a central angle. The length of a circular arc is calculated by the direct ratio of the central angle and the length of the entire circle. The central angle of 360° corresponds to the length of the whole circle, 180° to half of the circle's circumference, etc. A circular arc and two radii creates a geometric shape called a circular segment.Direction: Solve each problem carefully and show your solution in each item.
Number of problems found: 78
- Central angle 2
 What is the arc length of a circle with a radius of 12 cm and a central angle of 255 degrees? A. 8.5 cm B. 12π cm C. 24π cm D. 17π cm
What is the arc length of a circle with a radius of 12 cm and a central angle of 255 degrees? A. 8.5 cm B. 12π cm C. 24π cm D. 17π cm - Two wipers
 What A car has two wipers which do not overlap. Each wiper has a blade of length 21 cm, sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades.
What A car has two wipers which do not overlap. Each wiper has a blade of length 21 cm, sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades. - Circle graph
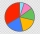 Erica surveyed students at her school about their favorite type of music. She made a circle graph to show the results. The central angle for the section of the graph that represents country music measures 72°. If 45 classmates chose the country as their f
Erica surveyed students at her school about their favorite type of music. She made a circle graph to show the results. The central angle for the section of the graph that represents country music measures 72°. If 45 classmates chose the country as their f - Velocipedes
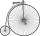 In the 19th century, bicycles had no chain drive, and the wheel axis connected the pedals directly. This wheel diameter gradually increased until the so-called high bikes (velocipedes) had a front-wheel diameter of up to 1.5 meters, while the rear wheel w
In the 19th century, bicycles had no chain drive, and the wheel axis connected the pedals directly. This wheel diameter gradually increased until the so-called high bikes (velocipedes) had a front-wheel diameter of up to 1.5 meters, while the rear wheel w - The bridge
 A vehicle weighing 5,800 kg passes 41 km/h on an arched bridge with a radius of curvature of 62 m. What force pushes the car onto the bridge as it passes through the center? What maximum speed can it cross over the bridge's center so it does not fly off t
A vehicle weighing 5,800 kg passes 41 km/h on an arched bridge with a radius of curvature of 62 m. What force pushes the car onto the bridge as it passes through the center? What maximum speed can it cross over the bridge's center so it does not fly off t - Describes 55223
 The minute hand is 30 cm long. The hour hand is half as short as the minute hand. How big a track describes its endpoint in a week.
The minute hand is 30 cm long. The hour hand is half as short as the minute hand. How big a track describes its endpoint in a week. - Half-circles 81731
 A skier skis down a black slope. He makes a total of 31 half-circles while going down the hill. The radius of one semicircle is 4m. What distance did he travel?
A skier skis down a black slope. He makes a total of 31 half-circles while going down the hill. The radius of one semicircle is 4m. What distance did he travel? - Semicircular 83449
 A fish in a semicircular aquarium with a radius of 1-meter swims close to its round wall. How many times does he swim back and forth if he swims a total distance of 94.2 m?
A fish in a semicircular aquarium with a radius of 1-meter swims close to its round wall. How many times does he swim back and forth if he swims a total distance of 94.2 m? - Acceleration
 Describe how the cyclist's acceleration changes on individual sections (sections AB plane, BC turn, CD plane, DA turn), which describes the trajectory in the shape of an eight at a constant speed. The speed on the cyclist's tachometer is constant.
Describe how the cyclist's acceleration changes on individual sections (sections AB plane, BC turn, CD plane, DA turn), which describes the trajectory in the shape of an eight at a constant speed. The speed on the cyclist's tachometer is constant. - Relative 8009
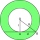 Sketch the relative position of the circles k1 (S1, r1 = 5cm) and k2 (S2, r2 = 3cm) and k / S1S2 / = 0 cm and give its name.
Sketch the relative position of the circles k1 (S1, r1 = 5cm) and k2 (S2, r2 = 3cm) and k / S1S2 / = 0 cm and give its name. - Square and circles
 The square in the picture has a side length of a = 20 cm. Circular arcs have centers at the vertices of the square. Calculate the areas of the colored unit. Express area using side a.
The square in the picture has a side length of a = 20 cm. Circular arcs have centers at the vertices of the square. Calculate the areas of the colored unit. Express area using side a. - Clocks
 What distance will describe the tip of a minute hand 6 cm long for 20 minutes when we know the starting position with finally enclosed hands at each other at 120°?
What distance will describe the tip of a minute hand 6 cm long for 20 minutes when we know the starting position with finally enclosed hands at each other at 120°? - The big clock
 The big clock hands stopped at a random moment. What is the probability that: a) a small hand showed the time between 1:00 and 3:00. b) the big hand was in the same area as a small hand in the role of a)? c) did the hours just show the time between 21:00
The big clock hands stopped at a random moment. What is the probability that: a) a small hand showed the time between 1:00 and 3:00. b) the big hand was in the same area as a small hand in the role of a)? c) did the hours just show the time between 21:00 - Determine 54881
 On the tourist map with a scale of 1:50000, the section of the railway line between Bobrová Lhota and Javořiště is replaced by an arc of a circle with a radius of 6 cm. The arc is 90°. Determine the actual length of the track between the two villages.
On the tourist map with a scale of 1:50000, the section of the railway line between Bobrová Lhota and Javořiště is replaced by an arc of a circle with a radius of 6 cm. The arc is 90°. Determine the actual length of the track between the two villages. - Minute hand
 What is the distance the clock's minute hand travels in 12 minutes if the clock's diameter is 30 cm and the hand extends to a distance of 2 cm from the edge of the clock?
What is the distance the clock's minute hand travels in 12 minutes if the clock's diameter is 30 cm and the hand extends to a distance of 2 cm from the edge of the clock? - Perimeter 59
 The perimeter of a circular bed is 36m. Find the length of the part of its perimeter that corresponds to the given central angles: 90°, 45°30', 120°, 15°
The perimeter of a circular bed is 36m. Find the length of the part of its perimeter that corresponds to the given central angles: 90°, 45°30', 120°, 15° - Corresponding 7621
 The length of the circular arc at the corresponding angle of 120 ° is 8 cm. What is the size of the whole circle? What is its radius?
The length of the circular arc at the corresponding angle of 120 ° is 8 cm. What is the size of the whole circle? What is its radius? - Calculate 7111
 Calculate the length of the arc, which will describe the endpoint of a longer hand 10 cm long wall clock after 20 minutes.
Calculate the length of the arc, which will describe the endpoint of a longer hand 10 cm long wall clock after 20 minutes. - Running
 The length of the inner edge of the running oval is 400 m. The straight sections measure 90 m. Calculate the dimensions of the oval - the rectangle where this oval can fit.
The length of the inner edge of the running oval is 400 m. The straight sections measure 90 m. Calculate the dimensions of the oval - the rectangle where this oval can fit. - Circumference - bed
 The perimeter of the round bed is 36m. Find the length of the part of its circumference that belongs to the given center angles of 180°
The perimeter of the round bed is 36m. Find the length of the part of its circumference that belongs to the given center angles of 180°
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
