Circular arc practice problems - last page
Direction: Solve each problem carefully and show your solution in each item.Number of problems found: 78
- Circular arc
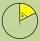 Calculate the center angle and length of the circular arc if the radius r = 21 cm and the area of the slice is 328.5 cm²
Calculate the center angle and length of the circular arc if the radius r = 21 cm and the area of the slice is 328.5 cm² - Flakes
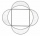 A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips?
A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips? - Quadrilateral in circle
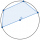 A quadrilateral is inscribed in the circle. Its vertices divide the circle in a ratio of 1:2:3:4. Find the sizes of its interior angles.
A quadrilateral is inscribed in the circle. Its vertices divide the circle in a ratio of 1:2:3:4. Find the sizes of its interior angles. - Circumferential 8399
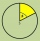 A circle with a radius r=8 cm is divided by points K and L in a ratio of 5 to 4. Calculate the sizes of the center and circumferential angles, corresponding to both arcs and the area of the larger segment.
A circle with a radius r=8 cm is divided by points K and L in a ratio of 5 to 4. Calculate the sizes of the center and circumferential angles, corresponding to both arcs and the area of the larger segment. - The circle arc
 Calculate the span of the arc, which is part of a circle with diameter d = 11 m and its height is 5 m.
Calculate the span of the arc, which is part of a circle with diameter d = 11 m and its height is 5 m. - A chord
 In a circle radius of 6 cm, a chord is drawn 3 cm from the center. Calculate the angle subtended by the chord at the center of the circle. Hence find the length of the minor arc cut off by the chord.
In a circle radius of 6 cm, a chord is drawn 3 cm from the center. Calculate the angle subtended by the chord at the center of the circle. Hence find the length of the minor arc cut off by the chord. - Circle section
 An equilateral triangle with side 33 is an inscribed circle section whose center is in one of the triangle's vertices, and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio between the circumference to the circle sector a
An equilateral triangle with side 33 is an inscribed circle section whose center is in one of the triangle's vertices, and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio between the circumference to the circle sector a - Equilateral triangle v3
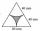 Find the area of the colored gray part. An equilateral triangle has a side length of 8 cm. Arc centers are the vertices of a triangle.
Find the area of the colored gray part. An equilateral triangle has a side length of 8 cm. Arc centers are the vertices of a triangle. - Determine 8010
 Determine the cone's base's radius if its shell develops into a circular section with radius "s" = 10 and center angle x = 60 °. r = ?, o =?
Determine the cone's base's radius if its shell develops into a circular section with radius "s" = 10 and center angle x = 60 °. r = ?, o =? - Colored area
 How large is the area colored brown inside a square of side 6 cm if each of the four brown circular segments is from a circle with a radius of the length of the square's side? The length of the circular segments is equal to the length of the side of the s
How large is the area colored brown inside a square of side 6 cm if each of the four brown circular segments is from a circle with a radius of the length of the square's side? The length of the circular segments is equal to the length of the side of the s - Circle and chord
 The chord of a circle is 233 long, and the length of the circular arc above the chord is 235. What is the circle's radius, and what is the central angle of the circular arc?
The chord of a circle is 233 long, and the length of the circular arc above the chord is 235. What is the circle's radius, and what is the central angle of the circular arc? - Convex angle
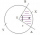 There is a circle k (S; r), and a point A, which lies on this circle. There is also a point B on the circumference, for which it is true that in one direction, it is five times further from point A than in the opposite direction (around the circumference
There is a circle k (S; r), and a point A, which lies on this circle. There is also a point B on the circumference, for which it is true that in one direction, it is five times further from point A than in the opposite direction (around the circumference - Arc and segment
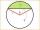 Calculate the length of circular arc l, the area of the circular arc S1, and the area of circular segment S2. The circle's radius is 88, and the corresponding angle is (4)/(7) π.
Calculate the length of circular arc l, the area of the circular arc S1, and the area of circular segment S2. The circle's radius is 88, and the corresponding angle is (4)/(7) π. - Circle arc
 The circle segment has a circumference of 9.08 km and 58.99 km² area. Calculate the radius of the circle and the size of the central angle.
The circle segment has a circumference of 9.08 km and 58.99 km² area. Calculate the radius of the circle and the size of the central angle. - Cone A2V
 The cone's surface in the plane is a circular arc with a central angle of 126° and an area of 415 cm². Calculate the volume of a cone.
The cone's surface in the plane is a circular arc with a central angle of 126° and an area of 415 cm². Calculate the volume of a cone. - Chord - TS
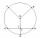 The radius of circle k measures 68 cm. Arc GH = 47 cm. What is TS?
The radius of circle k measures 68 cm. Arc GH = 47 cm. What is TS? - V-belt
 Calculate the length of the V-belt when the diameter of the pulleys is: D1 = 600 mm D2 = 120 mm d = 480 mm (distance between pulley axes)
Calculate the length of the V-belt when the diameter of the pulleys is: D1 = 600 mm D2 = 120 mm d = 480 mm (distance between pulley axes) - Circular segment
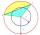 Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ)
Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ)
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
