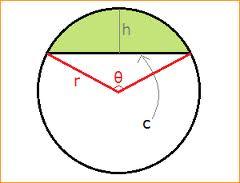
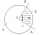
Arc and segment
Calculate the length of circular arc l, the area of the circular arc S1, and the area of circular segment S2. The circle's radius is 88, and the corresponding angle is .
Correct answer:
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- planimetrics
- circle
- area of a shape
- perimeter
- triangle
- circular sector
- circular segment
- goniometry and trigonometry
- sine
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Corresponding 59063
Calculate the radius and area of the circular segment if the center angle = 106° and the length of the corresponding circular arc is l = 52 cm. - Circumferential 8399
A circle with a radius r=8 cm is divided by points K and L in a ratio of 5 to 4. Calculate the sizes of the center and circumferential angles, corresponding to both arcs and the area of the larger segment. - Centimeters 83442
Calculate the length of the arc of a circle and the volume of a circular section if the circle's radius is 8.3 centimeters and the central angle alpha=104 degrees. - Circle arc
The circle segment has a circumference of 135.26 dm and 2096.58 dm² area. Calculate the radius of the circle and the size of the central angle.
- Corresponding 7621
The length of the circular arc at the corresponding angle of 120 ° is 8 cm. What is the size of the whole circle? What is its radius? - Circle's 81078
The chord of a circle is 233 long, and the length of the circular arc above the chord is 235. What is the circle's radius, and what is the central angle of the circular arc? - The length
The length of the circle is 24 cm. What is the circular arc length of the corresponding angle of 30°?
