Circumferential 8399
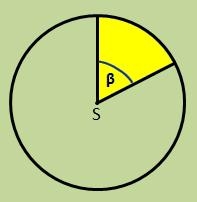
A circle with a radius r=8 cm is divided by points K and L in a ratio of 5 to 4. Calculate the sizes of the center and circumferential angles, corresponding to both arcs and the area of the larger segment.
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Circumferential angle
Vertices of the triangle ΔABC lay on the circle and are divided into arcs in the ratio 7:8:7. Determine the size of the angles of the triangle ΔABC. - Corresponding 59063
Calculate the radius and area of the circular segment if the center angle = 106° and the length of the corresponding circular arc is l = 52 cm. - Rhombus construction
Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides. - Connect 6500
Draw the line KL = 55mm. Draw a circle k with center K and radius 4cm. Mark the points to belong to the circle and connect them with point L. - Corresponding 82704
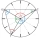On the circular face of the clock, we connect the points corresponding to the numbers 2, 5, and 9 to each other, which creates a triangle. Calculate the sizes of all interior angles. - Chord 2
Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle. - Tangents
To circle with a radius of 41 cm from the point R guided two tangents. The distance of both points of contact is 16 cm. Calculate the distance from point R and circle center. - Chord
It is given to a circle k(r=6 cm), and the points A and B such that |AB| = 8 cm lie on k. Calculate the distance of the center of circle S to the midpoint C of segment AB. - Ace
The length of segment AB is 24 cm, and the points M and N are divided into thirds. Calculate the circumference and area of this shape. - Two circles
Two circles with a radius of 4 cm and 3 cm have a center distance of 0.5cm. How many common points have these circles? - Annulus
The radius of the larger circle is 8cm, and the radius of the smaller is 5cm. Calculate the area of the annulus. - Corresponding 79314
On the circular face of the clock, we connect the points corresponding to the numbers 2, 9, and 11, which creates a triangle. Calculate the sizes of all the interior angles of that triangle. - Calculate 3167
The area of the two circles is in a 4: 9 ratio. The larger circle has a diameter of 12 cm. Calculate the radius of the smaller circle. - Touch circle
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - Calculate 12061
The area of the two circles is in a 4:9 ratio. The larger circle has a diameter of 18 cm. Calculate the radius of the smaller circle. - A spherical segment
The aspherical section, whose axial section has an angle of j = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the cut surface. - Calculate 82282
Calculate the sizes of the interior angles in the triangle whose vertices are the points marked by the numbers 1, 5, and 8 on the clock face.
