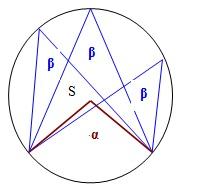
Circumferential angle
Vertices of the triangle ΔABC lay on the circle and are divided into arcs in the ratio 10:8:7.
Determine the size of the angles of the triangle ΔABC.
Determine the size of the angles of the triangle ΔABC.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
geometryplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Inscribed triangle
A circle is an inscribed triangle, and its vertices divide the circle into three arcs. The length of the arcs is in the ratio 2:3:7. Find the interior angles of a triangle. - Triangle in circle
The vertices of the triangle ABC lie on a circle with a radius 3, which is divided into three parts in the ratio 4:4:4. Calculate the circumference of the triangle ABC. - Construct 13581
The vertices of the triangle ABC lie on the circle k. The circle k is divided into three parts in a ratio of 1:2:3. Construct this triangle. - Angles of the triangle
ABC is a triangle. The size of the angles alpha and beta are in a ratio of 4:7. The angle gamma is greater than the angle alpha by a quarter of a straight angle. Determine the angles of the triangle ABC.
- Calculate 83431
In triangle ABC, the size of the exterior angle at vertex C is equal to 126°. The size of the internal angles at vertices A and B are in the ratio 5: 9. Calculate the size of the internal angles α, β, γ of triangle ABC. - The angles 4
The angles of a triangle are divided into the ratio 126: 213: 312. If the three angles sum to 180°, find the size of each of the three angles. - Circumferential 8399
A circle with a radius r=8 cm is divided by points K and L in a ratio of 5 to 4. Calculate the sizes of the center and circumferential angles, corresponding to both arcs and the area of the larger segment.
