Triangle in circle
The vertices of the triangle ABC lie on a circle with a radius 3, which is divided into three parts in the ratio 4:4:4.
Calculate the circumference of the triangle ABC.
Calculate the circumference of the triangle ABC.
Correct answer:
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Check out our ratio calculator.
See also our trigonometric triangle calculator.
Check out our ratio calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
planimetricsbasic operations and conceptsnumbersgoniometry and trigonometryGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Construct 13581
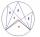
The vertices of the triangle ABC lie on the circle k. The circle k is divided into three parts in a ratio of 1:2:3. Construct this triangle. - Circumferential angle
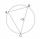
Vertices of the triangle ΔABC lay on the circle and are divided into arcs in the ratio 10:8:7. Determine the size of the angles of the triangle ΔABC. - MO - triangles
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a - Triangle 3552
Draw a circle k (S, r = 3cm). Build a triangle ABC so that its vertices lie on the circle k and the length of the sides is (AB) = 2.5 cm (AC) = 4 cm - Two-fifths 5337
The triangle is divided into three parts. The part at the vertex C occupies a third of the area of the triangle, the part at the vertex B is two-fifths of the area of the triangle, and the remaining part at the vertex A has an area of 4 m². Calculate the - Semicircles
In a rectangle with sides of 4cm and 8cm, there are two different semicircles, each of which has its endpoints at its adjacent vertices and touches the opposite side. Construct a square such that its two vertices lie on one semicircle, the remaining two o - A cone 4
A cone with a radius of 10 cm is divided into two parts by drawing a plane through the midpoint of its axis parallel to its base. Compare the volumes of the two parts.
