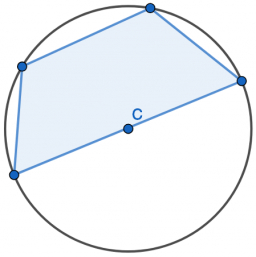
Quadrilateral in circle
A quadrilateral is inscribed in the circle. Its vertices divide the circle in a ratio of 1:2:3:4. Find the sizes of its interior angles.
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
geometryplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Inscribed triangle
 A circle is an inscribed triangle, and its vertices divide the circle into three arcs. The length of the arcs is in the ratio 2:3:7. Find the interior angles of a triangle.
A circle is an inscribed triangle, and its vertices divide the circle into three arcs. The length of the arcs is in the ratio 2:3:7. Find the interior angles of a triangle. - Interior angles
 In a quadrilateral ABCD, whose vertices lie on some circle, the angle at vertex A is 58 degrees, and the angle at vertex B is 134 degrees. Calculate the sizes of the remaining interior angles.
In a quadrilateral ABCD, whose vertices lie on some circle, the angle at vertex A is 58 degrees, and the angle at vertex B is 134 degrees. Calculate the sizes of the remaining interior angles. - Calculate 82282
 Calculate the sizes of the interior angles in the triangle whose vertices are the points marked by the numbers 1, 5, and 8 on the clock face.
Calculate the sizes of the interior angles in the triangle whose vertices are the points marked by the numbers 1, 5, and 8 on the clock face. - Clock face
 On the circular face of the clock, we connect the points corresponding to the numbers 2, 5, and 9 to each other, which creates a triangle. Calculate the sizes of all interior angles.
On the circular face of the clock, we connect the points corresponding to the numbers 2, 5, and 9 to each other, which creates a triangle. Calculate the sizes of all interior angles. - Calculate 68394
 The sizes of the interior angles of the triangle are in the ratio of 3:4:5. Calculate these angles.
The sizes of the interior angles of the triangle are in the ratio of 3:4:5. Calculate these angles. - Complementary 81152
 In a certain polygon, the ratio of the sum of the sizes of its internal angles and the sum of the sizes of the complementary angles is 2:5. How many vertices does this polygon have?
In a certain polygon, the ratio of the sum of the sizes of its internal angles and the sum of the sizes of the complementary angles is 2:5. How many vertices does this polygon have? - Corresponding 79314
 On the circular face of the clock, we connect the points corresponding to the numbers 2, 9, and 11, which creates a triangle. Calculate the sizes of all the interior angles of that triangle.
On the circular face of the clock, we connect the points corresponding to the numbers 2, 9, and 11, which creates a triangle. Calculate the sizes of all the interior angles of that triangle.
