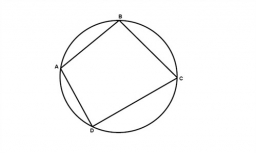
Interior angles
In a quadrilateral ABCD, whose vertices lie on some circle, the angle at vertex A is 58 degrees, and the angle at vertex B is 134 degrees. Calculate the sizes of the remaining interior angles.
Correct answer:
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Quadrilateral in circle
A quadrilateral is inscribed in the circle. Its vertices divide the circle in a ratio of 1:2:3:4. Find the sizes of its interior angles. - Calculate 82282
Calculate the sizes of the interior angles in the triangle whose vertices are the points marked by the numbers 1, 5, and 8 on the clock face. - In an
In an ABCD square, n interior points are chosen on each side. Find the number of all triangles whose vertices X, Y, and Z lie at these points and on different sides of the square. - Quadrilateral 82395
The points ABC lie on the circle k(S, r) such that the angle at B is obtuse. How large must the angle at vertex B of quadrilateral SCBA be so that this angle is three times greater than the interior angle ASC of the same quadrilateral?
- Calculate 11771
The interior angles of the triangle are 108 degrees 45 minutes and 51 degrees 19 minutes. Calculate the outside angle at the third vertex. - Quadrilateral 7583
For the sizes of the interior angles of the quadrilateral ABCD, the following applies: the angle alpha is 26° greater than the angle beta, twice the angle Beta is 5° less than the angle gamma, and the angle gamma is 36° greater than the angle delta. Deter - Clock hands
Calculate the internal angles of a triangle whose vertices lie on the clock's 2, 6, and 11 hours.
