Colored area
How large is the area colored brown inside a square of side 6 cm if each of the four brown circular segments is from a circle with a radius of the length of the square's side? The length of the circular segments is equal to the length of the side of the square. The situation is shown in the picture on the right.
Final Answer:

Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Square and circles
 The square in the picture has a side length of a = 20 cm. Circular arcs have centers at the vertices of the square. Calculate the areas of the colored unit. Express area using side a.
The square in the picture has a side length of a = 20 cm. Circular arcs have centers at the vertices of the square. Calculate the areas of the colored unit. Express area using side a. - Rafael
 Rafael has three squares. The first square has a side length of 2 cm. The second square has a side length of 4 cm, and its vertex is placed in the center of the first square. The last square has a side length of 6 cm, and its vertex is placed in the cente
Rafael has three squares. The first square has a side length of 2 cm. The second square has a side length of 4 cm, and its vertex is placed in the center of the first square. The last square has a side length of 6 cm, and its vertex is placed in the cente - Percentage 82623
 The square in the picture has a side length of 6 cm. What percentage of the area is the colored part?
The square in the picture has a side length of 6 cm. What percentage of the area is the colored part? - Chord 24
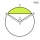 A chord with length t = r times the square root of two divides a circle with radius r into two circular segments. What is the ratio of the areas of these segments?
A chord with length t = r times the square root of two divides a circle with radius r into two circular segments. What is the ratio of the areas of these segments? - Integer 7814
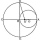 The small circle in the picture has an area of 3.5 cm². It touches from the inside and passes through the center of the large circle. What is the area of a large circle? The result round to an integer.
The small circle in the picture has an area of 3.5 cm². It touches from the inside and passes through the center of the large circle. What is the area of a large circle? The result round to an integer. - Circumscribed by triangle
 Inside the rectangle ABCD, the points E and F lie so that the line segments EA, ED, EF, FB, and FC are congruent. Side AB is 22 cm long, and the circle circumscribed by triangle AFD has a radius of 10 cm. Determine the length of side BC.
Inside the rectangle ABCD, the points E and F lie so that the line segments EA, ED, EF, FB, and FC are congruent. Side AB is 22 cm long, and the circle circumscribed by triangle AFD has a radius of 10 cm. Determine the length of side BC. - Equilateral triangle v3
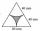 Find the area of the colored gray part. An equilateral triangle has a side length of 8 cm. Arc centers are the vertices of a triangle.
Find the area of the colored gray part. An equilateral triangle has a side length of 8 cm. Arc centers are the vertices of a triangle.
