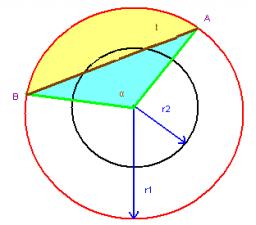
Circular segment

Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°.

Help formula: S = 1/2 r². (Β-sinβ)

Your answer:

Help us improve! If you spot a mistake, please let let us know. Thank you!

Tips for related online calculators

See also our right triangle calculator.
Do you want to convert area units?
Do you want to convert length units?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.

You need to know the following knowledge to solve this word math problem:

geometry

inscribed angle theorem

planimetry

Pythagorean theorem
right triangle
circle
area of a shape
perimeter
triangle
circular sector
circular segment

goniometry and trigonometry

sine

Units of physical quantities

unit conversion
area
length
angle

Grade of the word problem

high school

We encourage you to watch this tutorial video on this math problem: video1 video2

Related math problems and questions:

Circular segment
Calculate the radius and area of the circular segment if the center angle = 106° and the length of the corresponding circular arc is l = 52 cm.
Circular arc
Calculate the center angle and length of the circular arc if the radius r = 21 cm and the area of the slice is 328.5 cm²
Circular arc
Calculate the length of the circular arc if the diameter d = 20 cm and the angle alpha = 142 °
Two wipers
What A car has two wipers which do not overlap. Each wiper has a blade of length 21 cm, sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades.
Arc and segment
Calculate the length of circular arc l, the area of the circular arc S₁, and the area of circular segment S₂. The circle's radius is 88, and the corresponding angle is (4)/(7) π.
Length of the arc
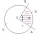What is the arc length of a circle k (S, r=68 mm), which belongs to a central angle of 78°?
Circle arc segment
A circle with a radius r=8 cm is divided by points K and L in a ratio of 5 to 4. Calculate the sizes of the center and circumferential angles, corresponding to both arcs and the area of the larger segment.