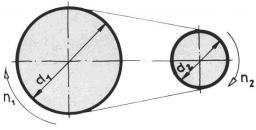
V-belt
Calculate the length of the V-belt when the diameter of the pulleys is:
D1 = 600 mm
D2 = 120 mm
d = 480 mm (distance between pulley axes)
Your answer:
D1 = 600 mm
D2 = 120 mm
d = 480 mm (distance between pulley axes)
Your answer:
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryplanimetrygoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- V-belt
Calculate the length of a belt running on two pulleys with diameters of 105 mm and 393 mm, with a centre-to-centre distance of 697 mm. - Engine pulley
The engine has a 1460 rev/min (RPM). The disc diameter is 350 mm. What will be the peripheral disc speed in RPM? Pulleys on the engine have a diameter of 80 mm, and a disc has a diameter of 160 mm. - Rectangle sides
Calculate the length of the side of the rectangle if you know its perimeter and the other side: a) o = 100 m: b = 2.5 m b) o = 80 cm: a = 20 mm c) o = 38.6 dm: b = 45 cm d) o = 88 mm: a = 2.5 cm - The ABCD
The ABCD trapezoid has a base length of a = 120 mm, c = 86 mm, and an area of S = 2575 mm². Calculate the height of the trapezoid. - Pulley
A fixed rope with a load is mounted on wheels with a diameter of 40 cm. Calculate how far the load is lifted when the wheel turns seven times. - Cuprum
From the 1600 mm long sheet of copper plate 2 mm thickness, we have separated over the whole length of the belt weighing 6000 g. Calculate belt width if one dm³ copper weighs 8.9 kg. - Washer
A washing machine drum spins at 64 RPM. The motor pulley has a diameter of 6 cm. What must be the diameter of the drum pulley if the motor runs at 367 RPM?
