Circle section
An equilateral triangle with side 33 is an inscribed circle section whose center is in one of the triangle's vertices, and the arc touches the opposite side.
Calculate:
a) the length of the arc
b) the ratio between the circumference to the circle sector and the perimeter of the triangle
Calculate:
a) the length of the arc
b) the ratio between the circumference to the circle sector and the perimeter of the triangle
Final Answer:

Tips for related online calculators
See also our right triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
planimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Equilateral triangle v3
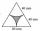 Find the area of the colored gray part. An equilateral triangle has a side length of 8 cm. Arc centers are the vertices of a triangle.
Find the area of the colored gray part. An equilateral triangle has a side length of 8 cm. Arc centers are the vertices of a triangle. - Math heart
 A stylized heart shape is created from a square with a 5 cm long side and two semicircles over its sides. Calculate the area and its circumference.
A stylized heart shape is created from a square with a 5 cm long side and two semicircles over its sides. Calculate the area and its circumference. - Circular segment
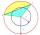 Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ)
Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ) - Determine 8010
 Determine the cone's base's radius if its shell develops into a circular section with radius "s" = 10 and center angle x = 60 °. r = ?, o =?
Determine the cone's base's radius if its shell develops into a circular section with radius "s" = 10 and center angle x = 60 °. r = ?, o =? - Eq triangle minus arcs
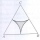 In an equilateral triangle with a 2cm long side, the arcs of three circles are drawn from the centers at the vertices and radii 1cm. Calculate the area of the shaded part - a formation that makes up the difference between the triangle area and circular cu
In an equilateral triangle with a 2cm long side, the arcs of three circles are drawn from the centers at the vertices and radii 1cm. Calculate the area of the shaded part - a formation that makes up the difference between the triangle area and circular cu - V-belt
 Calculate the length of the V-belt when the diameter of the pulleys is: D1 = 600 mm D2 = 120 mm d = 480 mm (distance between pulley axes)
Calculate the length of the V-belt when the diameter of the pulleys is: D1 = 600 mm D2 = 120 mm d = 480 mm (distance between pulley axes) - Circle arc + section
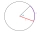 Calculate the length of the arc of a circle and the volume of a circular section if the circle's radius is 8.3 centimeters and the central angle alpha=104 degrees.
Calculate the length of the arc of a circle and the volume of a circular section if the circle's radius is 8.3 centimeters and the central angle alpha=104 degrees.
