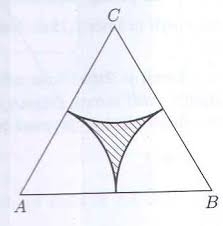
Eq triangle minus arcs
In an equilateral triangle with a 2cm long side, the arcs of three circles are drawn from the centers at the vertices and radii 1cm. Calculate the area of the shaded part - a formation that makes up the difference between the triangle area and circular cuts.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- intersection of sets
- planimetrics
- Pythagorean theorem
- right triangle
- circle
- area of a shape
- triangle
- circular arc
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Square and circles
The square in the picture has a side length of a = 20 cm. Circular arcs have centers at the vertices of the square. Calculate the areas of the colored unit. Express area using side a. - Equilateral triangle v3
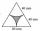Find the area of the colored gray part. An equilateral triangle has a side length of 8 cm. Arc centers are the vertices of a triangle. - Common chord
The common chord of the two circles c1 and c2 is 3.8 cm long. This chord forms an angle of 47° with the radius r1 of the circle c1 and an angle of 24° 30´ with the radius r2 of the circle c2. Calculate both radii and the distance between the two centers o - Intersect 6042
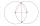Two circles with straight radii of 58 mm intersect at two points. Their common string is 80 mm long. What is the distance of the centers of these circles? - Intersections 2557
How many intersections do circles with radii of 10 cm and 6 cm have if the distance between their centers is 3 cm? - Circles
Three circles of radius 30 cm 28 cm and 37 cm are mutually tangent. What is the perimeter of the triangle whose vertices are centers of the circles? - Recursion squares
In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 22 cm. Calculate: a) the sum of peri - Circle section
Equilateral triangle with side 33 is inscribed circle section whose center is in one of the vertices of the triangle and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio betewwn the circumference to the circle sector and - Common chord
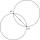Two circles with radius 17 cm and 20 cm are intersect at two points. Its common chord is long 27 cm. What is the distance of the centers of these circles? - Sidewalk 63134
There is a 2m wide sidewalk built around the circular fountain. The radii of the circles that delimit the path on both sides are 4: 3. What area in square meters does this sidewalk occupy? - Centimeters 7406
Circles with radii r1 = 10 centimeters and r2 = 4 cm touch from the outside. What is the distance of their centers? - The star
Find the area of the shaded part of square with a side of 22 cm. - Two parallel chords
In a circle 70 cm in diameter, two parallel chords are drawn so that the center of the circle lies between the chords. Calculate the distance of these chords if one of them is 42 cm long and the second 56 cm. - Equilateral triangle
How long should the minimum radius of the circular plate be cut an equilateral triangle with side 19 cm from it? - Calculate
Calculate the length of a side of the equilateral triangle with an area of 50cm². - Difference 66354
A circle is inscribed in a square with a side of 12 cm so that it touches all its sides. Calculate the difference between the area of the square and the circle. - Equilateral 35073
Draw an equilateral triangle ABC with a side of 8.5 cm. Assemble all the mines and measure them. What is the difference between the longest and the shortest of them?
