Acceleration
Describe how the cyclist's acceleration changes on individual sections (sections AB plane, BC turn, CD plane, DA turn), which describes the trajectory in the shape of an eight at a constant speed. The speed on the cyclist's tachometer is constant.
Correct answer:
Tips for related online calculators
Do you want to convert velocity (speed) units?
You need to know the following knowledge to solve this word math problem:
planimetricsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Isosceles 2588
Given an isosceles trapezoid ABCD, in which | AB | = 2 | BC | = 2 | CD | = 2 | DA | holds. On its side BC, the point K is such that | BK | = 2 | KC |; on its CD side, the point L is such that | CL | = 2 | LD |, and on its DA side, the point M is such that - Quadrilateral calc
The square ABCD is given. The midpoint of AB is E, the midpoint of BC is F, CD is G, and the midpoint of DA is H. Join AF, BG, CH, and DE. Inside the square (approximately in the middle), the intersections of these line segments form a quadrilateral. Calc - One trapezium
One trapezium has AB=24M, BC=36M, CD=80M, DA=80M long sides. Find the area. - Pentagon
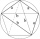The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm
- Tachometer
Tatra's tachometer shows the initial state 886123 km this morning. Today, Tatra travels at an average speed of 44 km/h. Determine the function that describes the Tatra's tachometer depending on the time. What is the state of the tachometer after 4 hours? - Internal angles
The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det - Perpendicularly 81951
A body of mass 4g is shot perpendicularly from the ground and lands in 8s. What is its kinetic energy at the beginning of its trajectory, what speed does it take off, and where does the distance from the ground stop? Thank you
