Isosceles 2588
Given an isosceles trapezoid ABCD, in which | AB | = 2 | BC | = 2 | CD | = 2 | DA | holds. On its side BC, the point K is such that | BK | = 2 | KC |; on its CD side, the point L is such that | CL | = 2 | LD |, and on its DA side, the point M is such that | DM | = 2 | MA |. Determine the sizes of the interior angles of the KLM triangle.
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
planimetricsUnits of physical quantitiesthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Internal angles
The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det - Triangle ABP
An isosceles trapezoid ABCD is given. The length of side AB is 10 cm, the length of CD is 7 cm, and the height to side AB is 4 cm. Point P is the base of the altitude to side AD. Calculate the area of the triangle ABP. - Trapezoid 4908
Trapezoid ABCD with bases AB = a, CD = c has height v. The point S is the center of the arm BC. Prove that the area of the ASD triangle is equal to half the area of the ABCD trapezoid. - Isosceles 37621
In the isosceles trapezoid ABCD, its bases AB = 20cm, CD = 12cm and arms AD = BC = 8cm are given. Specify its height and alpha angle at vertex A - One trapezium
One trapezium has AB=24M, BC=36M, CD=80M, DA=80M long sides. Find the area. - Trapezoid: 18703
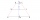In the ABCD trapezoid: | AD | = | CD | = | BC | a | AB | = | AC |. Determine the size of the delta angle. - Triangle ABC
There is the triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC tr
