Annulus practice problems
An annulus is a planar structure bounded by two concentric circles with different radii r1 and r2. It is a set of points whose distance from the common center S is between r1 and r2 inclusive. The area of the circle is the difference in the areas of the larger circle with radius r2 and the smaller circle with radius r1. In other words, an annulus is the intersection of circles with a common center and different radii.Direction: Solve each problem carefully and show your solution in each item.
Number of problems found: 49
- Geometric Solid
A concrete pipe is 1.0 m long. The inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (in cubic meters) needed to make 25 pieces of pipe? - Laurent series
Expand the function f (z) into the Laurent series at point z0 for the given annulus. f (z) = 1 / ((z-2) * (z-3)) a) z0 = 2, 0 3 - Concentric circles
There is given a Circle K with a radius r = 8 cm. How large must a radius have a smaller concentric circle that divides the circle K into two parts with the same area? - Concentric 6751
A circle K with radius r = 8 cm is given. How big a radius must a smaller concentric circle divides a circle K into two parts with the same area? - Insulation
A special rubber pipe protector is used to insulate the supply pipes of solar collectors. The product with the description DNa20, thickness 25 mm, 2 m, corresponds to insulation for pipes with a diameter of 20 mm with a rubber layer thickness of 25 mm, wh - Pipe cross section
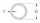The pipe has an outside diameter of 1100 mm, and the pipe wall is 100 mm thick. Calculate the cross-section of this pipe. - Annulus
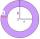Two concentric circles form an annulus with a width of 10 cm. The radius of the smaller circle is 20 cm. Calculate the area of the annulus.
- Shooter
The probability that a good shooter hits the center of the target circle No. I is 0.1. The probability that the target hit the inner circle II is 0.58. What is the probability that it hits the target circle I or II? - The pipe
The pipe is 1.5 m long. Its outer diameter is 60 cm, inner diameter is 52 cm. Calculate the pipe's weight if the material's density from which it is made is 2 g/cm³. Please round the results to whole kilograms. - Reinforcement 42491
The concrete ring (used for reinforcement in wells) has an inner diameter of 800 mm and an outer diameter of 900 mm. It is made of concrete with a density of 2,500 kg/m³. Its height is 1 m. Calculate its mass. - Annulus
Calculate the area of two circles annulus k1 (S, 3 cm) and k2 (S, 5 cm). - Calculate 8891
Calculate the weight of a PVC pipe with an inner diameter d = 45 mm and a length l = 3 m if the wall thickness of the pipe is s = 7.5 mm. The density of PVC is ρ = 1350 kg/m³. - Mass
The thickness of a metallic tube is 1cm, and its outer radius is 11cm. Find the mass of such a 1m long tube if the metal density is 7.5g per cubic cm. - Annulus
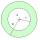The radius of the larger circle is 8cm, and the radius of the smaller is 5cm. Calculate the area of the annulus. - Brass sphere
Find the weight of a brass ball with an outer radius of 12 cm and a wall thickness of 20 mm if the brass's density is 8.5 g/cm³.
- Pipe thickness
The outer circumference of the tube is 32cm. Its length is 60cm, its density is 8.5g/cm3, and its weight is 9.495kg. Calculate the wall thickness of the pipe. - Approximately 28431
On the 200th anniversary of the birth of Ľudovít Štúr, the National Bank of Slovakia issued a commemorative two-euro coin in 2015, the diameter of which is 25.75 mm. The nickel-brass center is approximately 18 millimeters in diameter; the rest of the coin - Tablecloth's 28511
The round tabletop has a capacity of 2.01 m². Calculate the diameter of the round tablecloth if it exceeds the table's edge by 25 cm. - Two annuluses The area of the annular circle formed by two circles with a common center is 100 cm². The radius of the outer circle is equal to twice the radius of the inner circle. Determine the outside circle radius in centimeters.
- Round skirt The cut on the round skirt has the shape of an annulus. Determine how much m² of fabric will be consumed on an 80 cm long skirt. The waist circumference is a circle with a smaller radius of 69 cm.
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
See also more information on Wikipedia.
