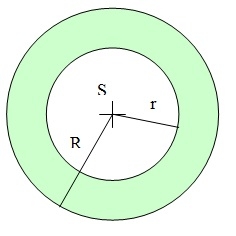
Concentric circles
There is given a Circle K with a radius r = 8 cm. How large must a radius have a smaller concentric circle that divides the circle K into two parts with the same area?
Correct answer:
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Concentric 6751
A circle K with radius r = 8 cm is given. How big a radius must a smaller concentric circle divides a circle K into two parts with the same area? - Annulus
Two concentric circles form an annulus of a width of 10 cm. The radius of the smaller circle is 20 cm. Calculate the area of the annulus. - Circular flowerbed
We split the circular flowerbed with diameter 8 m by concentric circle to circle and annulus with the same area. Find the radius of the circle. - Geodesist
Triangle-shaped field (triangle ABC) has a side AB = 129 m. path XY is parallel to the side AB, which divides triangle ABC into two parts with the same area. What will be the length of path XY? Help, please, geodesist. - An electricfan
An electric fan has a piece of wire 4 3/8 centimeters long. She divides the wire into parts that are 1 2/3 centimeters long. How many pieces does she have? - Circle annulus
There are two concentric circles in the figure. The chord of the larger circle, 10 cm long, is tangent to the smaller circle. What does annulus have? - MO Z8–I–6 2018
In the KLMN trapeze, KL has a 40 cm base and an MN of 16 cm. Point P lies on the KL line so that the NP segment divides the trapezoid into two parts with the same area. Find the length of the KP line. - Trapezoid thirds
The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment. - Concentric circles
In the circle with diameter, 13 cm is constructed chord 1 cm long. Calculate the radius of a concentric circle that touches this chord. - Eight
Eight small Christmas balls with a radius of 1 cm have the same volume as one large Christmas ball. What has a bigger surface: eight small balls or one big ball? - Maximally 4036
Mr. Novák wants to pave the terrace with tiles of two sizes to be as small as possible. Its terrace is square with a side 3 meters long. There is a wall of the house on two sides of the terrace. Next to the wall, he wants to put small tiles, the rest larg - Two circles
Two circles with the same radius, r = 1, are given. The center of the second circle lies on the circumference of the first. What is the area of a square inscribed in the intersection of given circles? - Belongs 8412
Given a circle k(O; 2.5 cm), a line p: /Op/=4 cm, a point T: T belongs to p and at the same time /OT/=4.5 cm. We must find all the circles that will touch the circle k and the line p at point T. - Calculate 5391
Viktor shot darts into a circular target with a radius of 5 cm. Inside the circle is a smaller circle with a radius of 2 cm. Calculate Viktor's chance of hitting a smaller circle in percent. - Circumscribed 29561
Construct an isosceles triangle if a given circle circumscribed with a radius r = 2.6 cm is given. - Wheels
A small tractor wheel with a diameter of 60 cm must be rotated eight times to overcome some pathways. How many times must you turn the big tractor wheel with a radius of 60 cm to overcome the same distance? - Measured 4046
Peter cut the two bars into equal parts but made them as large as possible. One rod measured 42 cm, the other 63 cm. How many cuts did he have to make?
