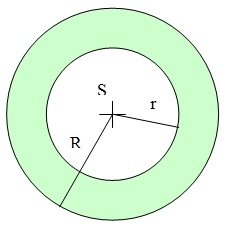
Circle annulus

There are 2 concentric circles in the figure. Chord of larger circle 10 cm long is tangent to the smaller circle. What are does annulus have?

Correct answer:

S =  78.5398 cm²

Step-by-step explanation:

$$\begin{gathered} R^2=(10\mathrm{/}2{)}^2+r^2 \\ {R}^2-r^2=5^2 \\ S=\pi \cdot R^2-\pi \cdot r^2 \\ S=\pi \cdot (R^2-r^2) \\ S=\pi \cdot 5^2=3.1416\cdot 5^2=78.5398{\text{cm}}^2 \end{gathered}$$

Try another example

Related math problems and questions:

• Concentric circles and chord
  In a circle with a diameter d = 10 cm, a chord with a length of 6 cm is constructed. What radius have the concentric circle while touch this chord?
• Concentric circles
  In the circle with diameter 19 cm is constructed chord 9 cm long. Calculate the radius of a concentric circle that touches this chord.
• Tangent
  What distance is the tangent t of the circle (S, 4 cm) and the chord of this circle, which is 6 cm long and parallel to the tangent t?
• Concentric circles
  There is given a Circle K with a radius r = 8 cm. How large must a radius have a smaller concentric circle that divides the circle K into two parts with the same area?
• Annulus
  Two concentric circles form an annulus of width 10 cm. The radius of the smaller circle is 20 cm. Calculate the content area of the annulus.
• Circles
  In the circle with a radius 7.5 cm are constructed two parallel chord whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions write both).
• Common chord
  Two circles with radius 17 cm and 20 cm are intersect at two points. Its common chord is long 27 cm. What is the distance of the centers of these circles?
• Circle's chords
  In the circle there are two chord length 30 and 34 cm. The shorter one is from the center twice than longer chord. Determine the radius of the circle.
• Chord AB
  What is the chord AB's length if its distance from the center S of the circle k(S, 92 cm) is 10 cm?
• Circle chord
  Calculate the length of the chord of the circle with radius r = 10 cm, length of which is equal to the distance from the center of the circle.
• Two chords
  In a circle with a radius of 8.5 cm, two parallel chords are constructed, the lengths of which are 9 cm and 12 cm. Find the distance of the chords in a circle.
• Right triangle - ratio
  The lengths of the legs of the right triangle ABC are in ratio b = 2: 3. The hypotenuse is 10 cm long. Calculate the lengths of the legs of that triangle.
• Chord
  In a circle with radius r=60 cm is chord 4× longer than its distance from the center. What is the length of the chord?
• Two chords
  Calculate the length of chord AB and perpendicular chord BC to circle if AB is 4 cm from the center of the circle and BC 8 cm from the center of the circle.
• Chord circle
  The circle to the (S, r = 8 cm) are different points A, B connected segment /AB/ = 12 cm. AB mark the middle of S'. Calculate |SS'|. Make the sketch.
• Circle described
  The radius of the circle described to the right triangle with 6 cm long leg is 5 cm. Calculate the circumference of this triangle.
• Two parallel chords
  The two parallel chords of the circle have the same length of 6 cm and are 8 cm apart. Calculate the radius of the circle.