Mezikruží
Na obrázku jsou 2 soustředné kružnice. Tětiva větší kružnice s délkou 10 cm je tečnou menší kružnice. Jaký obsah má mezikruží?
Správná odpověď:
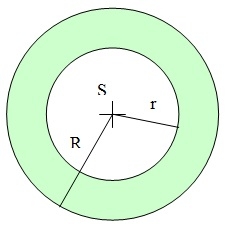
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraplanimetrieÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Mezikruží
 Dvě soustředné kružnice tvoří mezikruží šířky 10 cm. Poloměr menší kružnice je 20 cm. Vypočítejte obsah mezikruží.
Dvě soustředné kružnice tvoří mezikruží šířky 10 cm. Poloměr menší kružnice je 20 cm. Vypočítejte obsah mezikruží. - Soustředné kružnice
 Je dán kruh K s poloměrem r = 8 cm. Jak velký poloměr musí mít menší soustředná kružnice, která rozdělí kruh K na dvě části se stejným obsahem?
Je dán kruh K s poloměrem r = 8 cm. Jak velký poloměr musí mít menší soustředná kružnice, která rozdělí kruh K na dvě části se stejným obsahem? - Soustředna kružnice
 V kružnici s průměrem 16 cm je sestrojena tětiva délky 8 cm. Vypočtěte poloměr soustředné kružnice, která se dotýká tětivy.
V kružnici s průměrem 16 cm je sestrojena tětiva délky 8 cm. Vypočtěte poloměr soustředné kružnice, která se dotýká tětivy. - Soustředné kružnice
 Sestroj tři soustředné kružnice k, l, m se středem v bodě S a s poloměry 2cm, 3cm a 40mm
Sestroj tři soustředné kružnice k, l, m se středem v bodě S a s poloměry 2cm, 3cm a 40mm - Tětiva
 Jakou vzdálenost mají tečna t kružnice (S, 4 cm) a tětiva této kružnice, která má délku 6 cm a je rovnoběžná s tečnou?
Jakou vzdálenost mají tečna t kružnice (S, 4 cm) a tětiva této kružnice, která má délku 6 cm a je rovnoběžná s tečnou? - Těleso
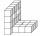 Těleso na obrázku je složeno z krychliček s délkou hrany 12 cm. Jaký povrch má toto těleso?
Těleso na obrázku je složeno z krychliček s délkou hrany 12 cm. Jaký povrch má toto těleso? - Kruhový záhon 2
 Kolem kruhové travnaté plochy je 2 m široký chodník. Vnější okraj chodníku tvoří obrubník, jehož délka je 157 m. Obrubník i vnitřní strana chodníku spolu tvoří soustředné kružnice. Vypočtěte obsah kruhové travnaté plochy a výsledek zaokrouhlete na desítky
Kolem kruhové travnaté plochy je 2 m široký chodník. Vnější okraj chodníku tvoří obrubník, jehož délka je 157 m. Obrubník i vnitřní strana chodníku spolu tvoří soustředné kružnice. Vypočtěte obsah kruhové travnaté plochy a výsledek zaokrouhlete na desítky
