Medzikružie 6
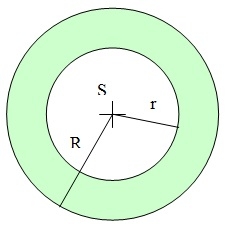
Na obrázku sú 2 sústredné kružnice. Tetiva väčšej kružnice s dĺžkou 10 cm je dotyčnicou menšej kružnice. Aký obsah má medzikružie?
Vaša odpoveď:
Vaša odpoveď:
Zobrazujem 2 komentáre:
Dr Math
Dlzka tetivy - jej polovica vytvara spolu s polomerom kruznice pravouhly trojuholnik. Tretia strana je vzdialenost tetivy od stredu kruznice.
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraplanimetriaÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Medzikružie
Dve sústredné kružnice tvoria medzikružie šírky 10 cm. Polomer menšej kružnice je 20 cm. Vypočítaj obsah medzikružia. - Sústredné kružnice
Je daný kruh K s polomerom r = 8 cm. Aký veľký polomer musí mať menšia sústredná kružnica, ktorá rozdelí kruh K na dve časti s rovnakým obsahom? - Sústredné kružnice 2
Zostroj tri sústredné kružnice k, l, m so stredom v bode S a s polomermi 2 cm, 3 cm a 40 mm - Gotický
Gotický štvorlístok je ornament, v ktorom sú do väčšej kružnice vpísané štyri rovnaké dotýkajúce sa menšie kružnice, ako vidíte na obrázku. Polomer veľkej kružnice je jeden meter. Vypočítajte v metroch polomer menšej kružnice. - Sústredné kruhy
Je daný kruh K s polomerom r=8 cm. Aký veľký polomer musí mať menšia sústredná kružnica, ktorá rozdelí kruh K na dve časti s rovnakým obsahom? - Trávnata plocha
Okolo kruhovej trávnatej plochy je 2 m široký chodník. Vonkajší okraj chodníka tvorí obrubník, ktorého dĺžka je 157 m. Obrubník aj vnútorná strana chodníku spolu tvoria sústredné kružnice. Vypočítajte obsah kruhovej trávnatej plochy a výsledok zaokrúhlite - Tetiva 17
Akú vzdialenosť majú dotyčnica t kružnice (S, 4 cm) a tetiva tejto kružnice, ktorá má dĺžku 6 cm a je rovnobežná s dotyčnicou?
