Geodesist
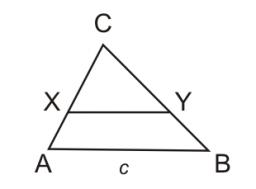
Triangle-shaped field (triangle ABC) has a side AB = 129 m. path XY is parallel to the side AB, which divides triangle ABC into two parts with the same area.
What will be the length of path XY? Help, please, geodesist.
What will be the length of path XY? Help, please, geodesist.
Final Answer:
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our trigonometric triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryalgebraarithmeticplanimetricsgoniometry and trigonometryGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Trapezoid thirds
The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment. - Triangle ABC
There is the triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC tr - Similarity of triangles
If triangle ABC ~ to triangle XYZ, AC = 24, AB = 15, BC = 17, and XY = 9, what is the perimeter of triangle XYZ? Round all sides to 1 decimal place. - Internal angles
The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det - MO - triangles
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a - 3 positive charges
Three equal positive charges Q are located at the vertices of an isosceles right triangle ABC. The right angle is at vertex A. The length of side AB is 1m. What is the electric field strength at the center S of side BC, i.e., what force would act on a pos - Segment in a triangle
In a triangle ABC with the side/AB/ = 24 cm constructed middle segment/DE/ = 18 cm parallel to the side AB at a distance of 1 cm from AB. Calculate the height of the triangle ABC to side AB.
