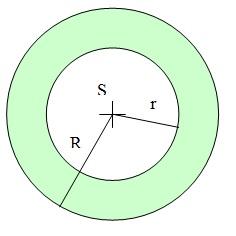
Two annuluses
The area of the annular circle formed by two circles with a common center is 100 cm2. The radius of the outer circle is equal to twice the radius of the inner circle. Determine the outside circle radius in centimeters.
Correct answer:
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Determine 12331
An annulus with an area S = 4.2 square meters has an inner radius r = 2.25 m. Determine the outer radius of the annulus. - Annular area
The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area. - Two circles
Two circles with a radius of 4 cm and 3 cm have a center distance of 0.5cm. How many common points have these circles? - Centimeters 7406
Circles with radii r1 = 10 centimeters and r2 = 4 cm touch from the outside. What is the distance between their centers?
- Circle chord
Determine the circle's radius in which the chord 6 cm away from the center is 12 cm longer than the circle's radius. - Chord 2
Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle. - Two circles
Two circles with the same radius, r = 1, are given. The center of the second circle lies on the circumference of the first. What is the area of a square inscribed in the intersection of given circles?
