Annular area
The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area.
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
planimetricsGrade of the word problem
Related math problems and questions:
- Circles
The area of a circle inscribed in a square is 7. What is the area of a circle circumscribed around a square? - Circles 2
Calculate the area bounded by the circumscribed and inscribed circle in a triangle with sides 29 cm, 16 cm, and 21 cm. - Two annuluses
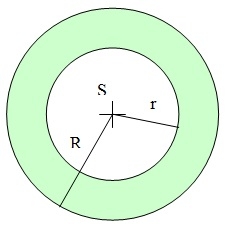
The area of the annular circle formed by two circles with a common center is 100 cm². The radius of the outer circle is equal to twice the radius of the inner circle. Determine the outside circle radius in centimeters. - RT and circles
Solve the right triangle if the radius of the inscribed circle is r=9 and the radius of the circumscribed circle is R=26. - Equation of the circle
Find the equation of the circle inscribed in the rhombus ABCD where A[1, -2], B[8, -3], and C[9, 4]. - Triangle - many properties
In a right triangle ABC with a right angle at the vertex C, it is given: a = 17cm, Vc = 8 cm. Calculate the length of the sides b, c, its area S, the perimeter o, the length of the radii of the circles of the triangle circumscribed by R and inscribed r an - Square and circles
Square with sides 68 km is circumscribed and inscribed with circles. Determine the radiuses of both circles.
