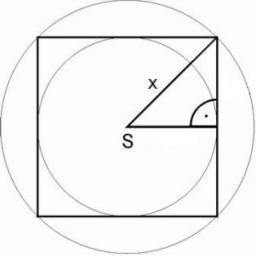
Square and circles
Square with sides 68 km is circumscribed and inscribed with circles. Determine the radiuses of both circles.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Circles 2
Calculate the area bounded by the circumscribed and inscribed circle in a triangle with sides 16 cm, 20 cm, and 15 cm. - Annular area
The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area. - Circles
The area of a circle inscribed in a square is 7. What is the area of a circle circumscribed around a square? - Triangle - many properties
In a right triangle ABC with a right angle at the vertex C, it is given: a = 17cm, Vc = 8 cm. Calculate the length of the sides b, c, its area S, the perimeter o, the length of the radii of the circles of the triangle circumscribed by R and inscribed r an
- Circumscription
Calculate the radius of the Circumscribed circle in the rectangle with sides 20 and 19. Can it be a rectangle inscribed by a circle? - RT and circles
Solve the right triangle if the radius of the inscribed circle is r=9 and the radius of the circumscribed circle is R=26. - Truncated cone 6
Calculate the volume of the truncated cone whose bases consist of an inscribed circle and a circle circumscribed to the opposite sides of the cube with the edge length a=1.
