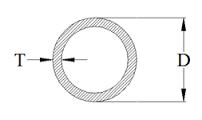
Pipe cross section
The pipe has an outside diameter of 1100 mm, and the pipe wall is 100 mm thick. Calculate the cross-section of this pipe.
Correct answer:
You need to know the following knowledge to solve this word math problem:
planimetricsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Cable
The cable consists of 8 strands, each strand consisting of 12 wires with a diameter of d = 0.5 mm. Calculate the cross-section of the cable. - Pipeline
How much percent has the pipe cross-section area changed (reduced) if the circular shape is changed to square with the same perimeter? - Plastic pipe
Calculate the plastic pipe's weight with diameter d = 100 mm and length 330 cm if the wall thickness is 4 mm and the density of plastic is 1346 kg/m³. - Calculate 8891
Calculate the weight of a PVC pipe with an inner diameter d = 45 mm and a length l = 3 m if the wall thickness of the pipe is s = 7.5 mm. The density of PVC is ρ = 1350 kg/m³. - Iron density
Calculate the weight of a 2 m long rail pipe with an internal diameter of 10 cm and a wall thickness of 3 mm. The iron density is p = 7.8 g/cm³. - Cross-section 82544
A water spray nozzle with a cross-section of 1.5 cm² sprays water at a speed of 24 m/s. What is the speed of the current in the supply pipe whose cross-section has a volume of 18 cm²? - Cross-section 47131
The 5 m long bar has a cross-section of an equilateral triangle with a side of 35 mm. Calculate its volume
