Iron density
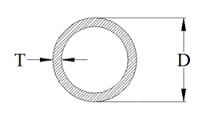
Calculate the weight of a 2 m long rail pipe with an internal diameter of 10 cm and a wall thickness of 3 mm. The iron density is p = 7.8 g/cm3.
Correct answer:
Tips for related online calculators
Do you want to convert length units?
Do you know the volume and unit volume, and want to convert volume units?
Tip: Our Density units converter will help you convert density units.
Do you want to convert mass units?
Do you know the volume and unit volume, and want to convert volume units?
Tip: Our Density units converter will help you convert density units.
Do you want to convert mass units?
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Themes, topics:
Grade of the word problem:
Related math problems and questions:
- Calculate 8891
Calculate the weight of a PVC pipe with an inner diameter d = 45 mm and a length l = 3 m if the wall thickness of the pipe is s = 7.5 mm. The density of PVC is ρ = 1350 kg/m³. - Plastic pipe
Calculate the plastic pipe's weight with diameter d = 100 mm and length 330 cm if the wall thickness is 4 mm and the density of plastic is 1346 kg/m³. - Hollow sphere
Calculate the weight of a hollow striebornej sphere (density 10.5 g/cm³) if the vnútorný diameter is 13 cm and the wall thickness is 5 mm. - Pipe thickness
The outer circumference of the tube is 32cm. Its length is 60cm, its density is 8.5g/cm3, and its weight is 9.495kg. Calculate the wall thickness of the pipe.
- Calculate 9981 The iron pipe has a length of 2m and a diameter of 4cm. If the density of iron is 7870 kg/m3, calculate its weight.
- The square
The square oak board (with density ρ = 700 kg/m3) has a side length of 50 cm and a thickness of 30 mm. 4 holes with a diameter of 40 mm are drilled into the board. What is the weight of the board? - Brass ball
What is the weight of a hollow brass ball, the outer diameter of which is 16 cm and the wall thickness is 2 cm, while the density of brass is ϱ = 8.5 g
