Triangle hypotenuse circle

In a right-angled triangle ABC with a right angle at the vertex C, the magnitudes of the hypotenuses are given ta=5, tb=2√10.
Calculate the side sizes of triangle ABC and the circle's radius described by this triangle.

Your answer:

Help us improve! If you spot a mistake, please let let us know. Thank you!

Tips for related online calculators

Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.

You need to know the following knowledge to solve this word math problem:

algebra

quadratic equation
equation
system of equations
rearrange variables

arithmetic

square root

planimetry

Pythagorean theorem
right triangle
triangle

Grade of the word problem

practice for 13 year olds
practice for 14 year olds

We encourage you to watch this tutorial video on this math problem: video1 video2

Related math problems and questions:

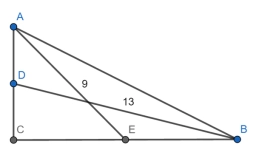
Median
In the ABC triangle is given side a=10 cm and median to side a: ta= 13 cm, and angle gamma 90°. Calculate the length of the median to side b (tb).
Triangle angle ratio
In the right-angled triangle ABC (the right angle at vertex C), the angle ratio is α : β = 5 : 3. Calculate the sizes of these angles and convert them to degrees and minutes (e.g., 45°20')
Triangle from median
Calculate the perimeter, area, and magnitudes of the triangle ABC's remaining angles: a = 8.4; β = 105° 35 '; and median ta = 12.5.
Perimeter triangle
In the triangle ABC, there is a side c = 5 cm and medians ta = 6 cm (median to side a), tb = 4.5 cm (median to side b). Find the perimeter of the triangle ABT (T = center of gravity).
Triangle angles
In triangle ABC, the interior angle at vertex B is 10 degrees greater than the angle at vertex A, and the angle at vertex C is three times greater than the angle at vertex B. Calculate the magnitudes of the interior angles of the triangle.
Similarity coefficient
The triangles ABC and A'B'C' are similar to the similarity coefficient 2. The sizes of the angles of the triangle ABC are α = 35° and β = 48°. Find the magnitudes of all angles of triangle A'B'C'.
Right-angled triangle
The right-angled triangle XYZ is similar to the triangle ABC, which has a right angle at the vertex X. The following applies: side a = 9 cm, x=4 cm, x = v-4 (v = height of triangle ABC). Calculate the unknown side lengths of both triangles.