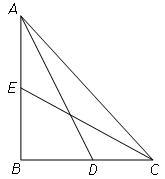
Median
In triangle ABC is given side a=10 cm and median ta= 13 cm and angle gamma 90°.
Calculate length of the median tb.
Calculate length of the median tb.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Perimeter 6002
In the triangle ABC there is a side c = 5cm and a medians ta = 6cm (median to side a), tb = 4.5cm (median to side b). Find the perimeter of the triangle ABT (T = center of gravity). - Triangle from median
Calculate the perimeter, area, and magnitudes of the triangle ABC's remaining angles, given: a = 8.4; β = 105° 35 '; and median ta = 12.5. - Triangle's centroid
In the triangle ABC the given lengths of its medians tc = 9, ta = 6. Let T be the intersection of the medians (triangle's centroid) and point is S the center of the side BC. The magnitude of the CTS angle is 60°. Calculate the length of the BC side to 2 d - Calculate 4425
In the triangle ABC with the center of gravity T, b = 7cm, median to c: tc = 9cm, the ATC angle is 112 degrees. Calculate the length of the line ta. - Medians 2:1
Median to side b (tb) in triangle ABC is 12 cm long. a. What is the distance of the center of gravity T from the vertex B? b, Find the distance between T and the side b. - Calculate 39031
In the triangle ABC, the line tb = | is given BB1 | Calculate the length of this line if B1T | = 3cm. - Medians in right triangle
It is given a right triangle, angle C is 90 degrees. I know it medians t1 = 8 cm and median t2 = 12 cm. .. How to calculate the length of the sides? - Calculate 4422
Calculate the perimeter of the triangle ABC if a = 12 cm, the angle beta is 38 degrees, and the gamma is 92 degrees. - There
There is a triangle ABC: A (-2,3), B (4, -1), C (2,5). Determine the general equations of the lines on which they lie: a) AB side, b) height to side c, c) Axis of the AB side, d) median ta to side a - Median in right triangle
In the rectangular triangle, ABC has known the length of the legs a = 15cm and b = 36cm. Calculate the length of the median to side c (to hypotenuse). - Calculate
Calculate the area of triangle ABC, if given by alpha = 49°, beta = 31°, and the height on the c side is 9cm. - Euclid2
In the right triangle ABC with a right angle at C is given side a=29 and height v=17. Calculate the perimeter of the triangle. - Perimeter of triangle
In the triangle, ABC angle A is 60° angle B is 90°, and side size c is 15 cm. Calculate the triangle circumference. - Gamma angle
Find the magnitude of the gamma angle in triangle ABC if: α = 38° 56 ’and β = 47° 54’. - Side c
In △ABC a=6, b=6 and ∠C=110°. Calculate the length of the side c. - The right triangle The right triangle ABC has a leg a = 36 cm and an area S = 540 cm². Calculate the length of the leg b and the median t2 to side b.
- Right triangle trigonometrics
Calculate the size of the remaining sides and angles of a right triangle ABC if it is given: b = 10 cm; c = 20 cm; angle alpha = 60° and the angle beta = 30° (use the Pythagorean theorem and functions sine, cosine, tangent, cotangent)
